Question

函数y=sin（cosx）的值域为（ ）
A．[-1，1]
B．[sin1，1]
C．[0，sin1]
D．[-sin1，sin1]

Answer 1

【答案】分析：首先确定函数y=sin（cosx）为复合函数，内函数cosx的值域为外函数y=sinx的定义域．然后求出cosx的值域，代入y=sinx即可求出函数y=sin（cosx）的值域．
解答：解：∵函数y=sin（cosx），
而cosx∈[-1，1]
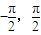
∴函数y=sinX在定义域[]里单调递增，
∴函数y=sin（cosx）的值域为：[-sin1，sin1]
故选：D
点评：本题考查复合函数的值域问题，涉及正弦函数的定义域以及值域，余弦函数的定义域以及值域问题，通过对复合函数的理解，分别求出余弦函数的值域以及正弦函数的值域即可解题，属于基础题．