
【题目】为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程。非一户一表用户电费采用“合表电价”收费标准:0.65元/度。“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
第一档 | 第二档 | 第三档 | |
每户每月用电量(单位:度) |
|
|
|
电价(单位:元/度) | 0.61 | 0.66 | 0.91 |
例如:某用户11月用电410度,采用合表电价收费标准,应交电费![]() 元,若采用阶梯电价收费标准,应交电费
元,若采用阶梯电价收费标准,应交电费![]() 元.
元.
为调查阶梯电价是否能取到“减轻居民负担”的效果,随机调查了该市100户的11月用电量,工作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量(单位:度)为:88、268、370、140、440、420、520、320、230、380.
组别 | 月用电量 | 频数统计 | 频数 | 频率 |
① |
|
| ||
② |
|
| ||
③ |
|
| ||
④ |
|
| ||
⑤ |
|
| ||
⑥ |
|
| ||
合计 |
(1)完成频率分布表,并绘制频率分布直方图;

(2)根据已有信息,试估计全市住户11月的平均用电量(同一组数据用该区间的中点值作代表);
(3)设某用户11月用电量为![]() 度(
度(![]() ),按照合表电价收费标准应交
),按照合表电价收费标准应交![]() 元,按照阶梯电价收费标准应交
元,按照阶梯电价收费标准应交![]() 元,请用
元,请用![]() 表示
表示![]() 和
和![]() ,并求当
,并求当![]() 时,
时,![]() 的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于75%的用户带来实惠?
的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于75%的用户带来实惠?
【答案】(1)见解析;(2)见解析(3)见解析
【解析】
(1)结合题意,完善表格,绘制频率直方图,即可。(2)结合数学期望计算方法,计算结果,估计平均数,即可。(3)结合题目信息,分别得到![]() 解析式,建立不等式,结合频率直方图,计算频率,即可。
解析式,建立不等式,结合频率直方图,计算频率,即可。
(1)频率分布表如下:
组别 | 月用电量 | 频数统计 | 频数 | 频率 |
① |
|
| 4 | 0.04 |
② |
|
| 12 | 0.12 |
③ |
|
| 24 | 0.24 |
④ |
|
| 30 | 0.3 |
⑤ |
|
| 26 | 0.26 |
⑥ |
|
| 4 | 0.4 |
合计 | 100 | 1 |
频率分布直方图如下:

(2)该100户用户11月的平均用电量
![]() 度
度
所以估计全市住户11月的平均用电量为324度.
(3)![]() ,
, .
.
由![]() 得
得![]() 或
或![]() 或
或![]() ,
,
解得![]() ,因
,因![]() ,故
,故![]() 的最大值为423根据频率分布直方图,
的最大值为423根据频率分布直方图,
![]() 时的频率为
时的频率为![]() ,
,
故估计“阶梯电价”能给不低于75%的用户带来实惠.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() ,
,![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() ,
,![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数![]() 的一种方法.例如:3可表示为“
的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用
”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用![]() 这9数字表示两位数的个数为
这9数字表示两位数的个数为![]()
![]()
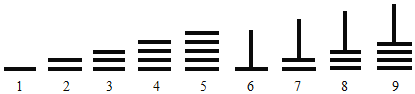
A.13B.14C.15D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
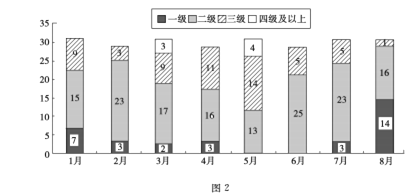
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与直线
两点,与直线![]() 相交于点
相交于点![]() ,且
,且![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中选
人中选![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?
,你有多大把握认为心肺疾病与性别有关?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:  ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点为A,B,点P,Q为椭圆上异于A,B的两点,直线AP、BP、BQ的斜率分别记为
的左右顶点为A,B,点P,Q为椭圆上异于A,B的两点,直线AP、BP、BQ的斜率分别记为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求证:
,求证:![]() ,并判断直线PQ是否过定点,若是,求出该定点;若不是,请说明理由.
,并判断直线PQ是否过定点,若是,求出该定点;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某电视台主办的歌手大奖赛上七位评委为甲、乙两名选手打出的分数的茎叶图(其中![]() 为数字0~9中的一个),则下列结论中正确的是( )
为数字0~9中的一个),则下列结论中正确的是( )
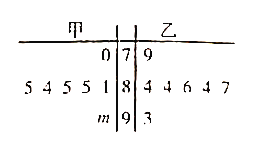
A. 甲选手的平均分有可能和乙选手的平均分相等
B. 甲选手的平均分有可能比乙选手的平均分高
C. 甲选手所有得分的中位数比乙选手所有得分的中位数低
D. 甲选手所有得分的众数比乙选手所有得分的众数高
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com