
【题目】已知非零实数![]() ,
,![]() ,
,![]() 不全相等,则下列说法正确的个数是( )
不全相等,则下列说法正确的个数是( )
(1)如果![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() ,
,![]() ,
,![]() 能构成等差数列
能构成等差数列
(2)如果![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() ,
,![]() ,
,![]() 不可能构成等比数列
不可能构成等比数列
(3)如果![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,![]() ,
,![]() 能构成等比数列
能构成等比数列
(4)如果![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,![]() ,
,![]() 不可能构成等差数列
不可能构成等差数列
A.1个B.2个C.3个D.4个
科目:高中数学 来源: 题型:
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
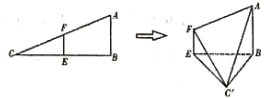
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,给定
,给定![]() 个整点
个整点![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,从上面的
时,从上面的![]() 个整点中任取两个不同的整点
个整点中任取两个不同的整点![]() ,求
,求![]() 的所有可能值;
的所有可能值;
(Ⅱ)从上面![]() 个整点中任取
个整点中任取![]() 个不同的整点,
个不同的整点,![]() .
.
(i)证明:存在互不相同的四个整点![]() ,满足
,满足![]() ,
,![]() ;
;
(ii)证明:存在互不相同的四个整点![]() ,满足
,满足![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九世纪末,法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”、“随机端点”、“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设A为圆O上一个定点,在圆周上随机取一点B,连接AB,所得弦长AB大于圆O的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,沿中位线DE折起后,点A对应的位置为点P,
,沿中位线DE折起后,点A对应的位置为点P,![]() .
.
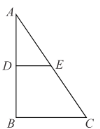
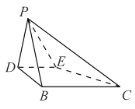
(1)求证:平面![]() 平面DBCE;
平面DBCE;
(2)求证:平面![]() 平面PCE;
平面PCE;
(3)求直线BP与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年7月27日上映以来,《战狼2》的票房一路高歌猛进,并不断刷新华语电影票房纪录.继8月25日官方宣布冲破53亿票房之后,根据外媒Worldwide Box Office给出的2017年周末全球票房最新排名,《战狼2》以8.151亿美元(约54.18亿元)的成绩成功杀入前五.通过收集并整理了《战狼2》上映前两周的票房(单位:亿元)数据,绘制出下面的条形图.根据该条形图,下列结论错误的是( )
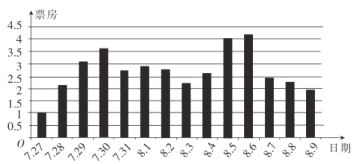
A.在《战狼2》上映前两周中,前四天票房逐日递增
B.在《战狼2》上映前两周中,日票房超过2亿元的共有12天
C.在《战狼2》上映前两周中,8月5日,8月6日达到了票房的高峰期
D.在《战狼2》上映前两周中,前五日的票房平均数高于后五日的票房平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com