练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）＝｜x－m｜－｜2x＋3m｜（m＞0）．

    （1）当m＝1时，求不等式f（x）≥1的解集；

    （2）对于任意实数x，t，不等式f（x）＜｜2＋t｜＋｜t－1｜恒成立，求m的取值范围．

    【答案】（1）； （2）.

    【解析】

    （1）将m=1的值带入，得到关于x的不等式组，求出不等式的解集即可；

    （2）问题等价于对任意的实数x,f（x）＜[|2+t|+|t﹣1|]min恒成立，根据绝对值的性质求出f（x）的最大值以及[|2+t|+|t﹣1|]min，求出m的范围即可．

    （1）当m=1时，.

    ，，或，或.

    解得：或，∴不等式的解集为.

    （2）不等式，对任意的实数t、x恒成立，

    等价于对任意的实数x，恒成立

    即.

    ∴函数单调递增，在单调递减，∴.

    又，又，所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)当时，求满足的的值；

    (2)若函数是定义在R上的奇函数，函数满足，若对任意且≠0,不等式恒成立，求实数m的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l过直线x﹣y﹣1=0与直线2x+y﹣5=0的交点P．

    （1）若l与直线x+3y﹣1=0垂直，求l的方程；

    （2）点A（﹣1，3）和点B（3，1）到直线l的距离相等，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一片森林原面积为，计划从某年开始，每年砍伐一些树林，且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时，所用时间是10年.为保护生态环境，森林面积至少要保留原面积的.已知到今年为止，森林剩余面积为原面积的.

    （1）求每年砍伐面积与上一年剩余面积的百分比；

    （2）到今年为止，该森林已砍伐了多少年？

    （3）为保护生态环境，今后最多还能砍伐多少年？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，等腰三角形PAD所在平面与菱形ABCD所在平面互相垂直，已知点E，F，M，N分别为边BA，BC，AD，AP的中点．

    （1）求证：AC⊥PE；

    （2）求证：PF∥平面BNM．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）若直角三角形两直角边长之和为12，求其周长的最小值；

    （2）若三角形有一个内角为，周长为定值，求面积的最大值；

    （3）为了研究边长满足的三角形其面积是否存在最大值，现有解法如下：（其中， 三角形面积的海伦公式），

    ∴

    ，

    而，，，则，

    但是，其中等号成立的条件是，于是与矛盾，

    所以，此三角形的面积不存在最大值．

    以上解答是否正确？若不正确，请你给出正确的答案．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】南京市自年成功创建“国家卫生城市”以来，已经连续三次通过“国家卫生城市”复审，年下半年，南京将迎来第四次复审.为了了解市民绿色出行的意识，现从某单位随机抽取名职工，统计了他们一周内路边停车的时间（单位：），整理得到数据分组及频率分布直方图如下：

    组号

    分组

    频数

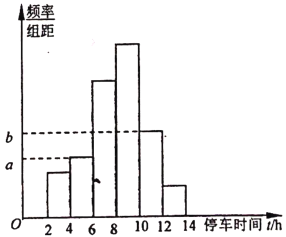
    （1）从该单位随机选取一名职工，试估计其在该周内路边停车的时间少于小时的概率；

    （2）求频率分布直方图中，的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正四棱锥S－ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动时，下列四个结论：①EP⊥AC；②EP∥BD；③EP∥平面SBD；④EP⊥平面SAC，其中恒成立的为( )

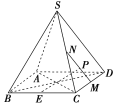
    A.①③B.③④C.①②D.②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设直线系M：xcosθ+（y﹣2）sinθ=1（0≤θ≤2π），对于下列四个命题：

    A．M中所有直线均经过一个定点

    B．存在定点P不在M中的任一条直线上

    C．对于任意整数n（n≥3），存在正n边形，其所有边均在M中的直线上

    D．M中的直线所能围成的正三角形面积都相等

    其中真命题的代号是 （写出所有真命题的代号）．

    查看答案和解析>>

    同步练习册答案