
 的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且
的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且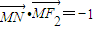 ,∠NMF2=120°.
,∠NMF2=120°.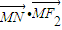 =(-a,b)•(c-a,0)=a2-ac=-1,由∠NMF2=120°,知∠NMF1=60°,故b=
=(-a,b)•(c-a,0)=a2-ac=-1,由∠NMF2=120°,知∠NMF1=60°,故b=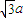 ,c=
,c=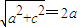 ,由此能求出双曲线的方程.
,由此能求出双曲线的方程.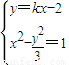 ,得(3-k2)x2+4kx-7=0,由此入手,能够求出的取值范围.
,得(3-k2)x2+4kx-7=0,由此入手,能够求出的取值范围.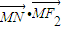 =(-a,b)•(c-a,0)=a2-ac=-1,
=(-a,b)•(c-a,0)=a2-ac=-1,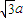 ,∴c=
,∴c=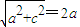 ,
,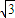 ,∴双曲线的方程为
,∴双曲线的方程为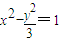 .(4分)
.(4分)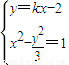 ,得(3-k2)x2+4kx-7=0,
,得(3-k2)x2+4kx-7=0,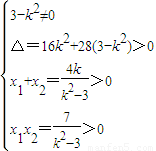 ,
,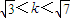 . ①(6分)
. ①(6分)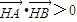 ,
,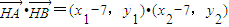
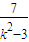 -(7+2k)•
-(7+2k)•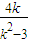 +53
+53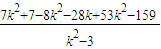 >0,解得k>2. ②
>0,解得k>2. ②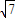 ,(8分)
,(8分)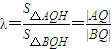 ,
,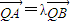 ,且λ>1,
,且λ>1,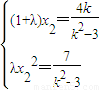 ,
,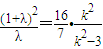 =
=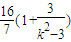 ,(10分)
,(10分)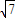 ,∴4<
,∴4<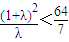 ,解得
,解得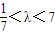 ,又λ>1,
,又λ>1,

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| MN |
| MF2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三4月模拟考试理科数学试卷(解析版) 题型:解答题
已知双曲线W: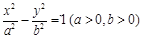 的左、右焦点分别为
的左、右焦点分别为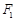 、
、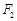 ,点
,点 ,右顶点是M,且
,右顶点是M,且 ,
, .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)过点 的直线l交双曲线W的右支于A、B两个不同的点(B在A、Q之间),若点
的直线l交双曲线W的右支于A、B两个不同的点(B在A、Q之间),若点 在以线段AB为直径的圆的外部,试求△AQH与△BQH面积之比λ的取值范围.
在以线段AB为直径的圆的外部,试求△AQH与△BQH面积之比λ的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省资阳市高三第二次高考模拟考试理科数学试卷 题型:解答题
已知双曲线W: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,点
,点 ,右顶点是M,且
,右顶点是M,且 ,
, .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)过点 的直线l交双曲线W的右支于A、B两个不同的点(B在A、Q之间),若点
的直线l交双曲线W的右支于A、B两个不同的点(B在A、Q之间),若点 在以线段AB为直径的圆的外部,试求△AQH与△BQH面积之比λ的取值范围.
在以线段AB为直径的圆的外部,试求△AQH与△BQH面积之比λ的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012年福建省漳州五中高考数学模拟试卷(理科)(解析版) 题型:解答题
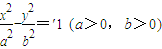 的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且
的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且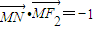 ,∠NMF2=120°.
,∠NMF2=120°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com