解:(1)f(x)=sin
2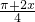
•4sinx+(cosx+sinx)•(cosx-sinx)
=4sinx•

+cos2x
=2sinx(1+sinx)+1-2sin
2x=2sinx+1,
∴f(x)=2sinx+1.
(2)∵f(ωx)=2sinωx+1,ω>0.
由2kπ-

≤ωx≤2kπ+

,
得f(ωx)的增区间是
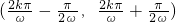
,k∈Z.
∵f(ωx)在
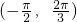
上是增函数,
∴
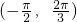
⊆

.
∴-

≥-
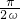
且

≤
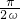
,
∴

.
(3)由|f(x)-m|<2,得-2<f(x)-m<2,即f(x)-2<m<f(x)+2.
∵A⊆B,∴当

≤x≤

时,
不等式f(x)-2<m<f(x)+2恒成立,
∴f(x)
min-2<m<f(x)
max+2,
∵f(x)
max=f(

)=3,f(x)
min=f(

)=2,
∴m∈(1,4).
分析:(1)通过数量积的计算,利用二倍角公式化简函数的表达式,化为一个角的一个三角函数的形式,即可.
(2)结合正弦函数的单调增区间,y=f(ωx)在区间
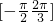
是增函数,说明
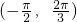
⊆

.求出ω的取值范围;
(3)简化集合B,利用A⊆B,得到恒成立的关系式,求出实数m的取值范围.
点评:本题是中档题,以向量的数量积为平台,考查三角函数的基本公式的应用,函数的单调性,以及函数的值域的求值范围,恒成立的应用,考查计算能力,转化思想.

 =
=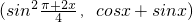 ,
, =(4sin x,cos x-sin x),f(x)=
=(4sin x,cos x-sin x),f(x)= •
• .
.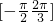 是增函数,求ω的取值范围;
是增函数,求ω的取值范围;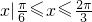 ,B={x||f(x)-m|<2},若A⊆B,求实数m的取值范围.
,B={x||f(x)-m|<2},若A⊆B,求实数m的取值范围.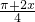 •4sinx+(cosx+sinx)•(cosx-sinx)
•4sinx+(cosx+sinx)•(cosx-sinx) +cos2x
+cos2x ≤ωx≤2kπ+
≤ωx≤2kπ+ ,
,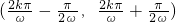 ,k∈Z.
,k∈Z.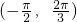 上是增函数,
上是增函数,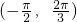 ⊆
⊆ .
. ≥-
≥-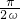 且
且 ≤
≤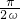 ,
, .
. ≤x≤
≤x≤ 时,
时, )=3,f(x)min=f(
)=3,f(x)min=f( )=2,
)=2,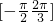 是增函数,说明
是增函数,说明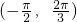 ⊆
⊆ .求出ω的取值范围;
.求出ω的取值范围;

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 如图,四边形ABCD中,E,F分别为AC、BD的中点,设向量
如图,四边形ABCD中,E,F分别为AC、BD的中点,设向量