(本小题满分13分)
如图,已知正三棱柱
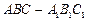
的底面正三角形的边长是2,D是
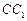
的中点,直线
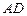
与侧面
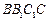
所成的角是
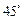
.
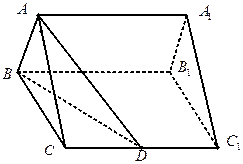
⑴求二面角
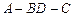
的大小;
⑵求点
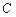
到平面
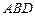
的距离.
解:⑴设侧棱长为
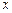
,取BC中点
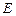
,则
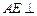
面

.∴
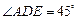
…2分
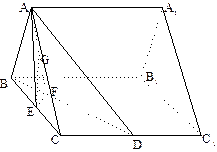
∴
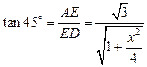
解得

…3分
过
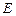
作

于

,连
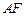
,
则

.
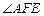
为二面角
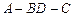
的平面角…5分
∵
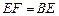

,
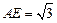
,
∴
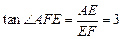
故二面角
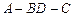
的大小
为
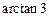
…7分
⑵由⑴知
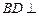
面
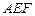
,∴面
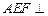
面
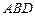
…9分
过
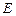
作
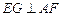
于
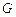
,则

面
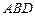
…11分
∴

∴
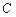
到面
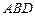
的距离为
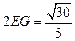
…13分

解法二:⑴求侧棱长

…3分如图建立空间直角坐标系,则
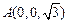
,
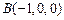
,
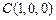
,
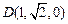
设
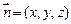
是平面
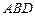
的一个法向量,则由
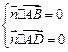
得
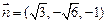
…5分而

是面
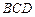
的一个法向量
∴

.而所求二面角为锐角,
即二面角
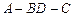
的大小为
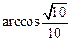
…8分
⑵∵

∴点
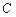
到面
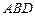
的距离为
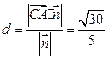
…12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:填空题
已知
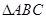
的三个顶点均在球O的球面上,且AB=AC=1,
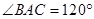
,直线OA与平面ABC所成的角的正弦值为
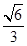
,则球面上B、C两点间的球面距离为
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(8分)
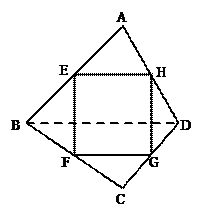
已知四边形
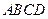
是空间四边形,
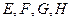
分别是边
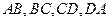
的中点,求证:四边形
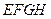
是平行四边形。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
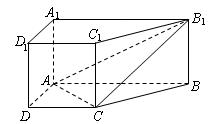
(本小题满分14分)直棱柱
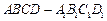
中,底面

是直角梯形,
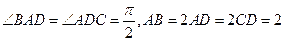
(Ⅰ)求证:
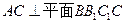
(Ⅱ)在

上是否存一点
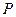
,使得

与平面
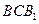
与平面
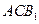
都平行?证明你的结论.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
(本小题满分12分)
如图,棱锥
P—
ABCD的底面
ABCD是矩形,
PA⊥平面
ABCD,
PA=
AD=2,
 BD
BD=
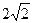
.
(1)求点
C到平面
PBD的距离.
(2)在线段
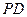
上是否存在一点
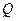
,使
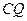
与平面
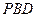
所成的角的正弦值为
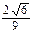
,若存在,指出点
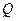
的位置,若不存在,说明理由.
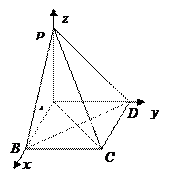
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知平面
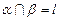
,
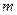
是
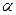
内不同于
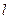
的直线,那么下列命题中错误的是
A

.若
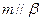
,则
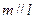
B.若
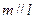
,则
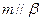
C.若
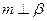
,则
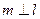
D.若
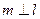
,则
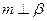
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
如图,E、F分别是正

方形
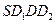
的边
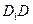
、

的中点,沿SE、SF、EF将它折成一个几何体,使
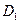
、D、

重合,记作D,给出下列位

置关系:
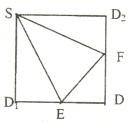
①SD
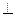
面EFD;②SE
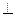
面EFD;③DF
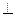
SE;④EF
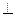
面SED其中成立的有( )
A.①与② B.①与③ C.②与③ D.③与④
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
如右图2,在二面角
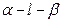
的棱

上有
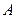
,
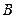
两点,直线
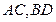
分别在这个二面角的两个半平面内,且都垂直于
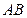
,若
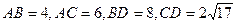
,则二面角
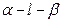
的大小为
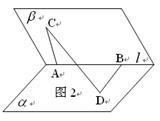
查看答案和解析>>

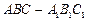 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是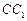 的中点,直线
的中点,直线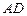 与侧面
与侧面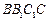 所成的角是
所成的角是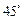 .
.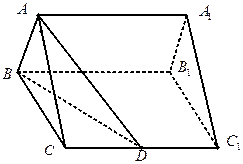
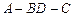 的大小;
的大小;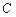 到平面
到平面 的距离.
的距离.  名校课堂系列答案
名校课堂系列答案 BD=
BD=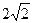 .
.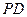 上是否存在一点
上是否存在一点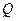 ,使
,使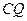 与平面
与平面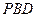 所成的角的正弦值为
所成的角的正弦值为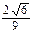 ,若存在,指出点
,若存在,指出点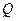 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.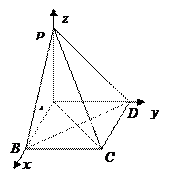
 方形
方形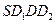 的边
的边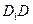 、
、 的中点,沿SE、SF、EF将它折成一个几何体,使
的中点,沿SE、SF、EF将它折成一个几何体,使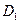 、D、
、D、 重合,记作D,给出下列位
重合,记作D,给出下列位 置关系:
置关系:
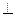 面EFD;②SE
面EFD;②SE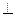 面EFD;③DF
面EFD;③DF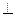 SE;④EF
SE;④EF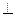 面SED其中成立的有( )
面SED其中成立的有( )