
【题目】已知函数f(x)=lnx+(e﹣a)x﹣b,其中e为自然对数的底数.若不等式f(x)≤0恒成立,则 ![]() 的最小值为 .
的最小值为 .
【答案】﹣ ![]()
【解析】解:∵函数f(x)=lnx+(e﹣a)x﹣b,其中e为自然对数的底数, ∴ ![]() ,x>0,
,x>0,
当a≤e时,f′(x)>0,
f(x)在(0,+∞)上是增函数,∴f(x)≤0不可能恒成立,
当a>e时,由 ![]() ,得x=
,得x= ![]() ,
,
∵不等式f(x)≤0恒成立,∴f(x)的最大值为0,
当x∈(0, ![]() )时,f′(x)>0,f(x)单调递增,
)时,f′(x)>0,f(x)单调递增,
当x∈( ![]() ,+∞)时,f′(x)<0,f(x)单调递减,
,+∞)时,f′(x)<0,f(x)单调递减,
∴当x= ![]() 时,f(x)取最大值,
时,f(x)取最大值,
f( ![]() )=﹣ln(a﹣e)﹣b﹣1≤0,
)=﹣ln(a﹣e)﹣b﹣1≤0,
∴ln(a﹣e)+b+1≥0,
∴b≥﹣1﹣ln(a﹣e),
∴ ![]() (a>e),
(a>e),
令F(x)= ![]() ,x>e,
,x>e,
F′(x)= 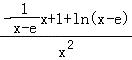 =
= ![]() ,
,
令H(x)=(x﹣e)ln(x﹣e)﹣e,
H′(x)=ln(x﹣e)+1,
由H′(x)=0,得x=e+ ![]() ,
,
当x∈(e+ ![]() ,+∞)时,H′(x)>0,H(x)是增函数,
,+∞)时,H′(x)>0,H(x)是增函数,
x∈(e,e+ ![]() )时,H′(x)<0,H(x)是减函数,
)时,H′(x)<0,H(x)是减函数,
∴当x=e+ ![]() 时,H(x)取最小值H(e+
时,H(x)取最小值H(e+ ![]() )=﹣e﹣
)=﹣e﹣ ![]() ,
,
∵x→e时,H(x)→0,x>2e时,H(x)>0,H(2e)=0,
∴当x∈(e,2e)时,F′(x)<0,F(x)是减函数,
当x∈(2e,+∞)时,F′(x)>0,F(x)是增函九,
∴x=2e时,F(x)取最小值,F(2e)= ![]() =﹣
=﹣ ![]() ,
,
∴ ![]() 的最小值为﹣
的最小值为﹣ ![]() .
.
故答案为:﹣ ![]() .
.
求出 ![]() ,x>0,当a≤e时,f′(x)>0,f(x)≤0不可能恒成立,当a>e时,由
,x>0,当a≤e时,f′(x)>0,f(x)≤0不可能恒成立,当a>e时,由 ![]() ,得x=
,得x= ![]() ,由题意当x=
,由题意当x= ![]() 时,f(x)取最大值0,推导出
时,f(x)取最大值0,推导出 ![]() (a>e),令F(x)=
(a>e),令F(x)= ![]() ,x>e,F′(x)=
,x>e,F′(x)= ![]() ,令H(x)=(x﹣e)ln(x﹣e)﹣e,H′(x)=ln(x﹣e)+1,由此利用导数性质能求出
,令H(x)=(x﹣e)ln(x﹣e)﹣e,H′(x)=ln(x﹣e)+1,由此利用导数性质能求出 ![]() 的最小值.
的最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 所在的半平面和直角梯形
所在的半平面和直角梯形![]() 所在的半平面成
所在的半平面成![]() 的二面角,
的二面角,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使锐二面角
,使锐二面角![]() 的余弦值为
的余弦值为![]() .若存在,请求出
.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴,与坐标系
轴为非负半轴为极轴,与坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有公共点,求倾斜角
有公共点,求倾斜角![]() 的取值范围;
的取值范围;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是古代中国劳动人民发明的一种中国传统智力玩具,它由五块等腰直角三角形,一块正方形和一块平行四边形共七块板组成.清陆以湉《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)是一直角墙角,![]() ,墙角的两堵墙面和地面两两互相垂直.
,墙角的两堵墙面和地面两两互相垂直.![]() 是一块长
是一块长![]() 为
为![]() 米,宽
米,宽![]() 为
为![]() 米的板材,现欲用板材与墙角围成一个直棱柱空间堆放谷物.
米的板材,现欲用板材与墙角围成一个直棱柱空间堆放谷物. 
(1)若按如图(1)放置,如何放置板材才能使这个直棱柱空间最大?
(2)由于墙面使用受限,![]() 面只能使用
面只能使用![]() 米,
米,![]() 面只能使用
面只能使用![]() 米.此矩形板材可以折叠围成一个直四棱柱空间,如图(2),如何折叠板材才能使这个空间最大?
米.此矩形板材可以折叠围成一个直四棱柱空间,如图(2),如何折叠板材才能使这个空间最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
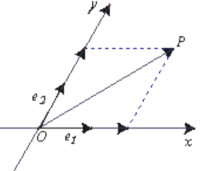
【题目】如图,设![]() 是平面内相交成
是平面内相交成![]() 角的两条数轴 ,
角的两条数轴 ,![]() 分别是
分别是![]() 轴,
轴,![]() 轴正方向同向的单位向量,若向量
轴正方向同向的单位向量,若向量![]() ,则把有序数对
,则把有序数对![]() 叫做向量
叫做向量![]() 在坐标系
在坐标系![]() 中的坐标,假设
中的坐标,假设![]() .
.
(1)计算![]() 的大小;
的大小;
(2)设向量![]() ,若
,若![]() 与
与![]() 共线,求实数
共线,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使得
,使得![]() 与向量
与向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知函数f(x)=ex, g(x)=lnx.
(1)设f(x)在x1处的切线为l1, g(x)在x2处的切线为l2,若l1//l2,求x1+g(x2)的值;
(2)若方程af 2(x)-f(x)-x=0有两个实根,求实数a的取值范围;
(3)设h(x)=f(x)(g(x)-b),若h(x)在[ln2,ln3]内单调递减,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com