
分析 (1)根据题意,由f(a+2)=81可得3a+2=81,解可得a的值,即可得函数g(x)的解析式,结合g(x)的解析式,先分析其定义域,再分析g(-x)与g(x)的关系,即可得答案;
(2)由(1)得到g(x)的解析式,将其变形可得g(x)=$\frac{2}{1+{2}^{x}}$-1,结合指数函数的性质分析即可得答案.
解答 解:(1)由f(a+2)=3a+2=81,得a+2=4,故a=2;
所以$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}$;
对于$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}$,其定义域为R,
而又由$g({-x})=\frac{{1-{2^{-x}}}}{{1+{2^{-x}}}}=\frac{{{2^x}-1}}{{{2^x}+1}}=-\frac{{1-{2^x}}}{{{2^x}+1}}=-g(x)$,
所以函数g(x)为奇函数;
(2)$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}=\frac{{2-(1+{2^x})}}{{1+{2^x}}}=\frac{2}{{1+{2^x}}}-1$,
${2^x}∈(0,+∞)⇒{2^x}+1∈(1,+∞)⇒\frac{1}{{{2^x}+1}}∈(0,1)$,
所以$\frac{2}{{{2^x}+1}}$$∈(0,2)⇒\frac{2}{{1+{2^x}}}-1∈(-1,1)$,
即函数g(x)的值域为(-1,1).
点评 本题考查函数的单调性、奇偶性的判定与应用,判定奇偶性之前要先分析函数的定义域.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{20}$ | |
| B. | $\frac{50}{1002}$ | |
| C. | $\frac{1}{1001}$ | |
| D. | 有两个个体与其它个体被抽到的概率不相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
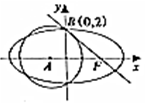 如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.
如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 3 | C. | 15 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
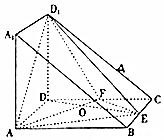 将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.
将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com