
| 3 |
| 2 |
| ||
| sin60° |
| c |
| sin(45°+30°) |
| ||||
| 2 |
| 1 |
| 2 |
3+
| ||
| 4 |
| ||
| sin60° |
| c |
| sin(45°+30°) |
| ||||
| 2 |
| ||||
| 2 |
3+
| ||
| 4 |
| 1 |
| 2 |
3+
| ||
| 4 |
| ||||||||||||||||
|
| ||||
| 2 |
3+
| ||
| 4 |
| ||
| sin60° |
| c |
| sin(45°+30°) |


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
| 3 |
| ||||
| 2 |
| ||||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| ||||
| 2 |
| ||||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
有一道解三角形的题因纸张破损,有一条件不清,且具体如下:在△ABC中,已知![]() ,B=
,B=![]() , ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=
, ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=![]() ,请将条件补完整.
,请将条件补完整.
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高一下学期期末理科数学试卷(解析版) 题型:选择题
有一道解三角形的题,因为纸张破损,在划横线地方有一个已知条件看不清.具体如下:在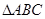 中角
中角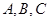 所对的边长分别为
所对的边长分别为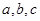 ,已知角
,已知角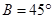 ,
,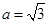 , ,求角
, ,求角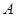 .若已知正确答案为
.若已知正确答案为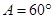 ,且必须使用所有已知条件才能解得,请你选出一个符合要求的已知条件.( )
,且必须使用所有已知条件才能解得,请你选出一个符合要求的已知条件.( )
A. B.
B.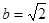
C.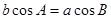 D.
D.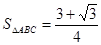
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com