定义在(-∞,+∞)上的奇函数f(x)和偶函数g(x)在区间(-∞,0]上的图象关于x轴对称,且f(x)为增函数,则下列各选项中能使不等式f(b)-f(-a)>g(a)-g(-b)成立的序号是________.
(1).a>b>0(2).a<b<0(3).ab>0 (4).ab<0.
解:由题得,不等式f(b)-f(-a)>g(a)-g(-b)?f(b)+f(a)>g(a)-g(b) 记为 ①
两个函数的大致图象为:
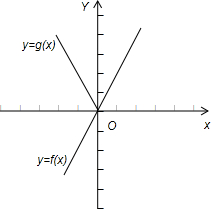
f(x),g(x)的图象在第一象限重合..
(1)当a>b>0时,f(a)=g(a)>f(b)=g(b)>f(0)=0?f(b)+f(a)=g(b)+g(a)>g(a)-g(b) 满足①.成立
(2)当a<b<0时,g(a)=-f(a)>0,g(b)=-f(b)>0,g(a)>g(b)?f(b)+f(a)=-g(a)-g(b)<g(a)-g(b) 不满足①舍
(3) 当ab>0,由(1)成立(2)不成立得(3)也不成立;
(4)当ab<0时,设a>0,b<0.则f(b)+f(a)=-g(b)+g(a)=g(a)-g(b) 不满足 ①舍.
故答案为:(1)..
分析:先把原不等式转化为f(b)+f(a)>g(a)-g(b),再利用条件画出两个函数的大致图象,结合图象对四个答案一一分析即可求出结果.
点评:本题主要考查函数的奇偶性与单调性,是对函数基本性质的综合考查,属于基础题.

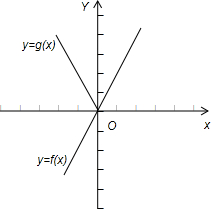 f(x),g(x)的图象在第一象限重合..
f(x),g(x)的图象在第一象限重合..
