
【题目】请你设计一个包装盒,![]() 是边长为
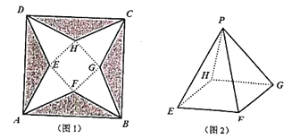
是边长为![]() 的正方形硬纸片(如图1所示),切去阴影部分所示的四个全等的等腰三角形,再沿虚线折起,使得
的正方形硬纸片(如图1所示),切去阴影部分所示的四个全等的等腰三角形,再沿虚线折起,使得![]() ,
,![]() ,
,![]() ,
,![]() 四个点重合于图2中的点
四个点重合于图2中的点![]() ,正好形成一个正四棱锥形状的包装盒(如图2所示),设正四棱锥
,正好形成一个正四棱锥形状的包装盒(如图2所示),设正四棱锥![]() 的底面边长为
的底面边长为![]() .
.
(1)若要求包装盒侧面积![]() 不小于
不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若要求包装盒容积![]() 最大,试问
最大,试问![]() 应取何值?并求出此时包装盒的容积.
应取何值?并求出此时包装盒的容积.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左右两个顶点,圆
的左右两个顶点,圆![]() 的半径为
的半径为![]() ,过点
,过点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,在
,在![]() 轴的上方交椭圆
轴的上方交椭圆![]() 于点
于点![]() .
.
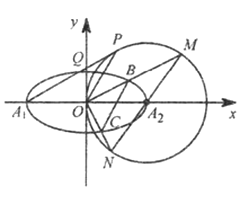
(1)求直线![]() 的方程;
的方程;
(2)求![]() 的值;
的值;
(3)设![]() 为常数,过点
为常数,过点![]() 作两条互相垂直的直线,分别交椭圆于点
作两条互相垂直的直线,分别交椭圆于点![]() ,分别交圆
,分别交圆![]() 于点
于点![]() ,记三角形
,记三角形![]() 和三角
和三角![]() 的面积分别为
的面积分别为![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其中a为常数,设e为自然对数的底数.
其中a为常数,设e为自然对数的底数.
(1)当![]() 时,求
时,求![]() 过切点为
过切点为![]() 的切线方程;
的切线方程;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求a的值;
,求a的值;
(3)若不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() .
.
(1)求椭圆的方程;
(2)点P,Q在椭圆![]() 上,O为坐标原点,且直线
上,O为坐标原点,且直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)直线l过点![]() 且与椭圆
且与椭圆![]() 交于A,B两点,问在x轴上是否存在定点M,使得
交于A,B两点,问在x轴上是否存在定点M,使得![]() 为常数?若存在,求出点M坐标以及此常数的值;若不存在,请说明理由.
为常数?若存在,求出点M坐标以及此常数的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,有下述命题:①若
,有下述命题:①若![]() 是奇函数,则
是奇函数,则![]() 的图象关于点
的图象关于点![]() 对称;②函数
对称;②函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 为偶函数;③若对
为偶函数;③若对![]() ,有
,有![]() ,则2是
,则2是![]() 的一个周期;④函数
的一个周期;④函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称.其中正确的命题是______.(写出所有正确命题的序号)
对称.其中正确的命题是______.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过![]() 分时,按
分时,按![]() 元/分计费;超过
元/分计费;超过![]() 分时,超出部分按
分时,超出部分按![]() 元/分计费.已知王先生家离上班地点
元/分计费.已知王先生家离上班地点![]() 公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间
公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间 ![]() (分)是一个随机变量.现统计了
(分)是一个随机变量.现统计了![]() 次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间 |
|
|
|
|
频数 |
|
|
|
|
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为![]() 分.(1)写出王先生一次租车费用
分.(1)写出王先生一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分)的函数关系式;(2)若王先生一次开车时间不超过
(分)的函数关系式;(2)若王先生一次开车时间不超过![]() 分为“路段畅通”,设
分为“路段畅通”,设![]() 表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.
表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 与
与![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且数列
,且数列![]() 是公比等于2的等比数列,求
是公比等于2的等比数列,求![]() 的值,使数列
的值,使数列![]() 也是等比数列;
也是等比数列;
(3)若![]() ,且
,且![]() ,数列
,数列![]() 有最大值
有最大值![]() 与最小值
与最小值![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(本题满分15分)已知m>1,直线![]() ,
,
椭圆![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线![]() 过右焦点
过右焦点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() ,
,
![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以线段
在以线段
![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com