
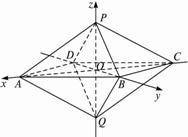
(1)证明PQ⊥平面ABCD;
(2)求异面直线AQ与PB所成的角;
(3)求点P到平面QAD的距离.
(1)证明:连结AC、BD,设AC∩BD=O.?
因为P—ABCD与Q—ABCD都是正四棱锥,?
所以PO⊥平面ABCD,QO⊥平面ABCD?
从而P、O、Q三点在一条直线上,所以PQ⊥平面ABCD.
(2)解:由题设知,ABCD是正方形,所以AC⊥BD,
由(1),PQ⊥平面ABCD,故可分别以直线CA、DB、QP为x轴、y轴、z轴建立空间直角坐标系(如下图),由题设条件,相关各点的坐标分别是P(0,0,1),A(2![]() ,0,0),Q(0,0,-2),B(0,2
,0,0),Q(0,0,-2),B(0,2![]() ,0).?
,0).?

所以![]() =(-2
=(-2![]() ,0,-2),
,0,-2),![]() =(0,2
=(0,2![]() ,-1),?
,-1),?
于是cos〈![]() ,
,![]() 〉=
〉=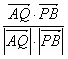 =
=![]() .?
.?
从而异面直线AQ与PB所成的角是arccos![]() .
.
(3)解:由(2),点D的坐标是(0,-2![]() ,0),?
,0),?
![]() =(-2
=(-2![]() ,-2
,-2![]() ,0),
,0),![]() =(0,0,-3).
=(0,0,-3).
设n=(x,y,z)是平面QAD的一个法向量,由?
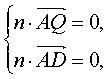 得
得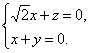
取x=1,得n=(1,-1,- ![]() ).?
).?
所以点P到平面QAD的距离?
d=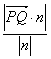 =
=![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
 我们将底面是正方形,侧棱长都相等的棱锥称为正四棱锥.已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同,且如图所示,视图中四边形ABCD是边长为1的正方形,则该几何体的体积为( )
我们将底面是正方形,侧棱长都相等的棱锥称为正四棱锥.已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同,且如图所示,视图中四边形ABCD是边长为1的正方形,则该几何体的体积为( )查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•奉贤区二模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.
(2008•奉贤区二模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
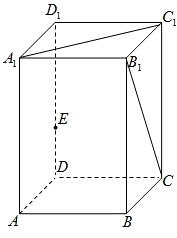 如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省福州三中高三(上)期中数学试卷(解析版) 题型:选择题





查看答案和解析>>
科目:高中数学 来源:2008年上海市奉贤区高考数学二模试卷(文科)(解析版) 题型:解答题
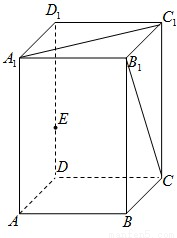
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com