
 如图,G是△OAB的重心,P,Q分别是边OA,OB上的动点(P点可以和A点重合,Q点可以与B点重合),且P,G,Q三点共线.
如图,G是△OAB的重心,P,Q分别是边OA,OB上的动点(P点可以和A点重合,Q点可以与B点重合),且P,G,Q三点共线.分析 (1)根据向量加法的三角形法则求解,即$\overrightarrow{OG}$=$\overrightarrow{OP}$+$\overrightarrow{PG}$;
(2)在△OPG和△OQG中分别利用正弦定理,得出$\frac{1}{x^2}$+$\frac{1}{y^2}$=$\frac{12}{a^2}$[1+$\frac{1}{2}$cos(2θ-$\frac{2π}{3}$)],再根据角θ的范围求得该式的最值.
解答 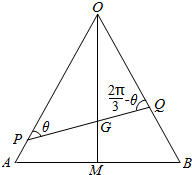 解:(1)根据向量加法的三角形法则,
解:(1)根据向量加法的三角形法则,
$\overrightarrow{OG}$=$\overrightarrow{OP}$+$\overrightarrow{PG}$=$\overrightarrow{OP}$+λ•$\overrightarrow{PQ}$=$\overrightarrow{OP}$+λ•($\overrightarrow{OQ}$-$\overrightarrow{OP}$)=(1-λ)$\overrightarrow{OP}$+λ$\overrightarrow{OQ}$,
即$\overrightarrow{OG}$=(1-λ)$\overrightarrow{OP}$+λ$\overrightarrow{OQ}$;
(2)如右图,设∠OPG=θ,因为三角形OAB为正三角形,且G为重心,
所以,当P在A处时,θ=$\frac{π}{6}$,当P在OA中点时,θ=$\frac{π}{2}$,
故θ∈[$\frac{π}{6}$,$\frac{π}{2}$],且∠OQG=$\frac{2π}{3}$-θ,
在△OPG中,由正弦定理得,$\frac{PG}{sin∠POG}$=$\frac{OG}{sinθ}$,
其中,PG=x,OG=$\frac{\sqrt{3}a}{3}$,解得x=$\frac{\sqrt{3}a}{6}$•$\frac{1}{sinθ}$,
在△OQG中,由正弦定理得,$\frac{QG}{sin∠QOG}$=$\frac{OG}{sin(\frac{2π}{3}-θ)}$,
其中,QG=y,OG=$\frac{\sqrt{3}a}{3}$,解得y=$\frac{\sqrt{3}a}{6}$•$\frac{1}{sin(\frac{2π}{3}-θ)}$,
所以,$\frac{1}{x^2}$+$\frac{1}{y^2}$=$\frac{12}{a^2}$•[sin2θ+sin2($\frac{2π}{3}$-θ)]
=$\frac{12}{a^2}$[1-$\frac{1}{2}$(cos2θ+cos($\frac{4θ}{3}$-2θ))]=$\frac{12}{a^2}$[1+$\frac{1}{2}$cos(2θ-$\frac{2π}{3}$)],
因为,θ∈[$\frac{π}{6}$,$\frac{π}{2}$],所以,2θ-$\frac{2π}{3}$∈[-$\frac{π}{3}$,$\frac{π}{3}$],
所以,cos(2θ-$\frac{2π}{3}$)∈[$\frac{1}{2}$,1],
故$\frac{1}{x^2}$+$\frac{1}{y^2}$∈[$\frac{15}{a^2}$,$\frac{18}{a^2}$].
点评 本题主要考查了向量的线性运算及其几何意义,以及运用正弦定理解三角形和三角函数最值的确定,属于难题.


科目:高中数学 来源: 题型:选择题
 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{6}}{4}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{\sqrt{19}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图(1),在Rt△ABC中,∠C=90°,BC=2,AC=4,点D,E分别是AC,AB的中点,将△ADE沿DE折起到△A1DE的位置,使A1D⊥DC如图(2)所示,M为A1D的中点,求CM与面A1EB所成角的正弦值.
如图(1),在Rt△ABC中,∠C=90°,BC=2,AC=4,点D,E分别是AC,AB的中点,将△ADE沿DE折起到△A1DE的位置,使A1D⊥DC如图(2)所示,M为A1D的中点,求CM与面A1EB所成角的正弦值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | 1-i | C. | -1+i | D. | -1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,定义在[-1,2]上的函数f(x)的图象为折线段ACB,
如图,定义在[-1,2]上的函数f(x)的图象为折线段ACB,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com