
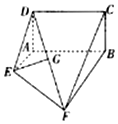
 ŅŃÖŖ¶ąĆęĢåABCDEFČēĶ¼ĖłŹ¾£¬ĘäÖŠABCDĪŖ¾ŲŠĪ£¬”÷DAEĪŖµČŃüµČŃüČż½ĒŠĪ£¬DA”ĶAE£¬ĖıߊĪAEFBĪŖĢŻŠĪ£¬ĒŅAE”ĪBF£¬”ĻABF=90”ć£¬AB=BF=2AE=2£®
ŅŃÖŖ¶ąĆęĢåABCDEFČēĶ¼ĖłŹ¾£¬ĘäÖŠABCDĪŖ¾ŲŠĪ£¬”÷DAEĪŖµČŃüµČŃüČż½ĒŠĪ£¬DA”ĶAE£¬ĖıߊĪAEFBĪŖĢŻŠĪ£¬ĒŅAE”ĪBF£¬”ĻABF=90”ć£¬AB=BF=2AE=2£®·ÖĪö £Ø1£©ŅŌBĪŖŌµć£¬BA£¬BF£¬BC·Ö±šĪŖxÖį£¬yÖį£¬zÖįÕż·½Ļņ£¬½ØĮ¢ČēĶ¼ĖłŹ¾µÄæÕ¼äÖ±½Ē×ų±źĻµ£¬Ēó³öĘ½ĆęABCDµÄŅ»øö·ØĻņĮ棬Ķعż$\overrightarrow{EG}•\overrightarrow n=£Ø-1£¬0£¬\frac{1}{2}£©•£Ø0£¬1£¬0£©=0$£¬ĶĘ³ö$\overrightarrow{EG}”Ķ\overrightarrow n$£¬¼“æÉÖ¤Ć÷EG”ĪĘ½ĆęABCD£®
£Ø2£©µ±µćNÓėµćDÖŲŗĻŹ±£¬Ö±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÓąĻŅÖµµČÓŚ$\frac{{\sqrt{21}}}{5}$£®ĄķÓÉČēĻĀ£ŗÖ±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÓąĻŅÖµĪŖ$\frac{{\sqrt{21}}}{5}$£¬¼“Ö±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÕżĻŅÖµĪŖ$\frac{2}{5}$£¬Ēó³öĘ½ĆęFCDµÄ·ØĻņĮ棬ÉčĻ߶ĪFDÉĻ“ęŌŚŅ»µćN£¬Ź¹µĆÖ±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÕżĻŅÖµµČÓŚ$\frac{2}{5}$£¬Éč$\overrightarrow{FN}=¦Ė\overrightarrow{FD}£Ø0”ܦĖ”Ü1£©$£¬ĶعżĻņĮæµÄŹżĮæ»ż£¬×Ŗ»ÆĒó½ā¦Ė£¬ĶĘ³öµ±NµćÓėDµćÖŲŗĻŹ±£¬Ö±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÓąĻŅÖµĪŖ$\frac{{\sqrt{21}}}{5}$£®
½ā“š 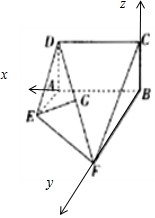 ½ā£ŗ£Ø1£©Ö¤Ć÷£ŗŅņĪŖDA”ĶAE£¬DA”ĶAB£¬AB”ÉAE=A£¬¹ŹDA”ĶĘ½ĆęABFE£¬
½ā£ŗ£Ø1£©Ö¤Ć÷£ŗŅņĪŖDA”ĶAE£¬DA”ĶAB£¬AB”ÉAE=A£¬¹ŹDA”ĶĘ½ĆęABFE£¬
¹ŹCB”ĶĘ½ĆęABFE£¬ŅŌBĪŖŌµć£¬BA£¬BF£¬BC·Ö±šĪŖxÖį£¬yÖį£¬zÖįÕż·½Ļņ£¬
½ØĮ¢ČēĶ¼ĖłŹ¾µÄæÕ¼äÖ±½Ē×ų±źĻµ£¬ŌņF£Ø0£¬2£¬0£©£¬D£Ø2£¬0£¬1£©£¬$G£Ø1£¬1£¬\frac{1}{2}£©$£¬E£Ø2£¬1£¬0£©£¬C£Ø0£¬0£¬1£©£¬ĖłŅŌ$\overrightarrow{EG}=£Ø-1£¬0£¬\frac{1}{2}£©$£¬Ņ×ÖŖĘ½ĆęABCDµÄŅ»øö·ØĻņĮæ$\overrightarrow n=£Ø0£¬1£¬0£©$£¬ĖłŅŌ$\overrightarrow{EG}•\overrightarrow n=£Ø-1£¬0£¬\frac{1}{2}£©•£Ø0£¬1£¬0£©=0$£¬ĖłŅŌ$\overrightarrow{EG}”Ķ\overrightarrow n$£¬ÓÖEG?Ę½ĆęABCD£¬ĖłŅŌEG”ĪĘ½ĆęABCD£®
£Ø2£©µ±µćNÓėµćDÖŲŗĻŹ±£¬Ö±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÓąĻŅÖµµČÓŚ$\frac{{\sqrt{21}}}{5}$£®ĄķÓÉČēĻĀ£ŗ
Ö±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÓąĻŅÖµĪŖ$\frac{{\sqrt{21}}}{5}$£¬¼“Ö±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÕżĻŅÖµĪŖ$\frac{2}{5}$£¬ŅņĪŖ$\overrightarrow{FD}=£Ø2£¬-2£¬1£©£¬\overrightarrow{CD}=£Ø2£¬0£¬0£©$£¬ÉčĘ½ĆęFCDµÄ·ØĻņĮæĪŖ$\overrightarrow{n_1}=£Ø{x_1}£¬{y_1}£¬{z_1}£©$£¬
ÓÉ$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{FD}=0\\ \overrightarrow{n_1}•\overrightarrow{CD}=0\end{array}\right.$£¬µĆ$\left\{\begin{array}{l}2{x_1}-2{y_1}+{z_1}=0\\ 2{x_1}=0\end{array}\right.$£¬Č”y1=1µĆĘ½ĆęFCDµÄŅ»øö·ØĻņĮæ$\overrightarrow{n_1}=£Ø0£¬1£¬2£©$
¼ŁÉčĻ߶ĪFDÉĻ“ęŌŚŅ»µćN£¬Ź¹µĆÖ±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÕżĻŅÖµµČÓŚ$\frac{2}{5}$£¬
Éč$\overrightarrow{FN}=¦Ė\overrightarrow{FD}£Ø0”ܦĖ”Ü1£©$£¬Ōņ$\overrightarrow{FN}=¦Ė£Ø2£¬-2£¬1£©=£Ø2¦Ė£¬-2¦Ė£¬¦Ė£©$£¬$\overrightarrow{BN}=\overrightarrow{BF}+\overrightarrow{FN}=£Ø2¦Ė£¬2-2¦Ė£¬¦Ė£©$£¬
ĖłŅŌ$sin¦Į=cos£¼\overrightarrow{BN}£¬\overrightarrow{n_1}£¾=\frac{{\overrightarrow{|BN}•\overrightarrow{n_1}|}}{{|\overrightarrow{BN}||\overrightarrow{n_1}|}}=\frac{2}{{\sqrt{5}•\sqrt{{{£Ø2¦Ė£©}^2}+{{£Ø2-2¦Ė£©}^2}+{¦Ė^2}}}}=\frac{2}{{\sqrt{5}•\sqrt{9{¦Ė^2}-8¦Ė+4}}}=\frac{2}{5}$£¬
ĖłŅŌ9¦Ė2-8¦Ė-1=0£¬½āµĆ¦Ė=1»ņ$¦Ė=-\frac{1}{9}$£ØÉįČ„£©
Ņņ“Ė£¬Ļ߶ĪDFÉĻ“ęŌŚŅ»µćN£¬µ±NµćÓėDµćÖŲŗĻŹ±£¬Ö±ĻßBNÓėĘ½ĆęFCDĖł³É½ĒµÄÓąĻŅÖµĪŖ$\frac{{\sqrt{21}}}{5}$£®
µćĘĄ ±¾Ģāæ¼²éæÕ¼äĻņĮæµÄÓ¦ÓĆ£¬Ö±ĻßÓėĘ½ĆęĘ½ŠŠŅŌ¼°Ö±ĻßÓėĘ½ĆęĖł³É½ĒµÄĒó·Ø£¬æ¼²éŹżŠĪ½įŗĻŅŌ¼°×Ŗ»ÆĖ¼ĻėµÄÓ¦ÓĆ£®


 ½šŌæ³×ŹŌ¾ķĻµĮŠ“š°ø
½šŌæ³×ŹŌ¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| Äź·Ż x | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 |
| ČĖŹż Y/ĶņČĖ | 55 196 | 56 300 | 57 482 | 58 796 | 60 266 | 61 560 | 62 828 | 64 563 | 65 994 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ×Ō2008ğʚ£¬ĆæÄźµÄÉś»īĄ¬»ųĪŽŗ¦»Æ“¦ĄķĮæŗĶÄź·Ż“śĀėÕżĻą¹Ų | |
| B£® | ×Ō2008ğʚ£¬ĆæÄźµÄÉś»īĄ¬»ųĪŽŗ¦»Æ“¦ĄķĮæ“óŌ¼Ōö¼Ó0.10Ķņ¶Ö | |
| C£® | ÓÉ“ĖÄ£ŠĶæÉÖŖ2016ÄźøƵŲĒųÉś»īĄ¬»ųĪŽŗ¦»Æ“¦ĄķĮæŹĒ1.82Ķņ¶Ö | |
| D£® | ÓÉ“ĖÄ£ŠĶŌ¤²ā³ö2017ÄźøƵŲĒųÉś»īĄ¬»ųĪŽŗ¦»Æ“¦ĄķĮæŌ¼ĪŖ1.92Ķņ¶Ö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
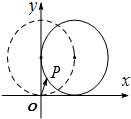 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ņ»µ„Ī»Ō²µÄŌ²ŠÄµÄ³õŹ¼Ī»ÖĆŌŚ£Ø0£¬1£©£¬“ĖŹ±Ō²ÉĻŅ»µćPµÄĪ»ÖĆŌŚ£Ø0£¬0£©£¬Ō²ŌŚxÖįÉĻŃŲÕżĻņ¹ö¶Æ£®µ±Ō²¹ö¶Æµ½Ō²ŠÄĪ»ÓŚ£Ø1£¬1£©Ź±£¬$\overrightarrow{OP}$µÄ×ų±źĪŖ£Ø””””£©
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ņ»µ„Ī»Ō²µÄŌ²ŠÄµÄ³õŹ¼Ī»ÖĆŌŚ£Ø0£¬1£©£¬“ĖŹ±Ō²ÉĻŅ»µćPµÄĪ»ÖĆŌŚ£Ø0£¬0£©£¬Ō²ŌŚxÖįÉĻŃŲÕżĻņ¹ö¶Æ£®µ±Ō²¹ö¶Æµ½Ō²ŠÄĪ»ÓŚ£Ø1£¬1£©Ź±£¬$\overrightarrow{OP}$µÄ×ų±źĪŖ£Ø””””£©| A£® | £Ø1-sin1£¬1-cos1£© | B£® | £Ø1+sin1£¬1-cos1£© | C£® | £Ø1-sin1£¬1+cos1£© | D£® | £Ø1+sin1£¬1+cos1£© |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ2015-2016ѧğ½Ī÷Ź”ÄĻ²żŹŠøßŅ»ĻĀŃ§ĘŚĘŚÄ©æ¼ŹŌŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗĢīæÕĢā
ŌŚÕż·½ŠĪÄŚÓŠŅ»ÉČŠĪ£Ø¼ūĶ¼ÖŠŅõÓ°²æ·Ö£©£¬µćPĖęŅāµČæÉÄÜĀäŌŚÕż·½ŠĪÄŚ£¬ŌņÕāµćĀäŌŚÉČŠĪĶā£¬ĒŅŌŚÕż·½ŠĪÄŚµÄøÅĀŹĪŖ________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 0 | B£® | 2 | C£® | 5 | D£® | 6 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 2 | B£® | $\sqrt{3}$ | C£® | 1 | D£® | $\frac{\sqrt{3}}{2}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com