
【题目】如图,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是线段EF上的动点
AC,P是线段EF上的动点
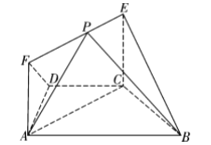
(1)求证:平面BCE⊥平面ACEF;
(2)求平面PAB与平面BCE所成锐二面角![]() 的最小值
的最小值
科目:高中数学 来源: 题型:
【题目】某投资公司计划投资![]() 、
、![]() 两种金融产品,根据市场调查与预测,
两种金融产品,根据市场调查与预测,![]() 产品的利润
产品的利润![]() 与投资量x成正比例,其关系如图1,
与投资量x成正比例,其关系如图1,![]() 产品的利润
产品的利润![]() 与投资量x的算术平方根成正比例,其关系如图2;(利润与投资量单位:万元)
与投资量x的算术平方根成正比例,其关系如图2;(利润与投资量单位:万元)
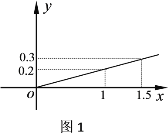
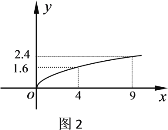
(1)分别将![]() 、
、![]() 两产品的利润表示为投资量的函数关系式;
两产品的利润表示为投资量的函数关系式;
(2)该公司已有20万元资金,并全部投入![]() 、
、![]() 两种产品中,问:怎样分配这20万元投资,才能使公司获得最大利润?其最大利润为多少万元?
两种产品中,问:怎样分配这20万元投资,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
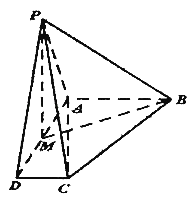
【题目】四棱锥P﹣ABCD中平面PAD⊥平面ABCD,AB∥CD,AB⊥AD,M为AD中点,PA=PD![]() ,AD=AB=2CD=2.
,AD=AB=2CD=2.
(1)求证:平面PMB⊥平面PAC;
(2)求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥AB,PA=1,PC=3,BC=2,sin∠PCA![]() ,E,F,G分别为线段的PC,PB,AB中点,且BE
,E,F,G分别为线段的PC,PB,AB中点,且BE![]() .
.
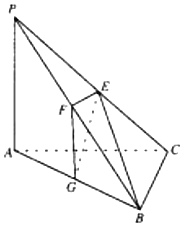
(1)求证:AB⊥BC;
(2)若M为线段BC上一点,求三棱锥M﹣EFG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,椭圆
,椭圆![]() 以
以![]() 的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆
的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆![]() 、
、![]() 上,若
上,若![]() ,则直线AB的斜率k为( ).
,则直线AB的斜率k为( ).
A.1B.-1C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 满足约束条件
满足约束条件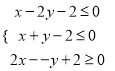 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为__________.
的值为__________.
【答案】![]() 或
或![]()
【解析】由题可知若![]() 取得最大值的最优解不唯一则
取得最大值的最优解不唯一则![]() 必平行于可行域的某一边界,如图:
必平行于可行域的某一边界,如图: 要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
点睛:线性规划为常考题型,解决此题务必要理解最优解个数为无数个时的条件是什么,然后根据几何关系求解即可
【题型】填空题
【结束】
16
【题目】《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别表示三角形的面积,大斜,中斜,小斜;
分别表示三角形的面积,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分别为对应的大斜,中斜,小斜上的高;则
分别为对应的大斜,中斜,小斜上的高;则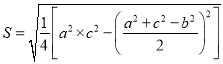
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根据上述公式,可以推出该三角形外接圆的半径为__________.
,根据上述公式,可以推出该三角形外接圆的半径为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为:
中,曲线C的参数方程为: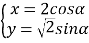 (
(![]() 为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)设点P的直角坐标为![]() ,若直线l与曲线C分别相交于A,B两点,求
,若直线l与曲线C分别相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是棱长为2的正方形,E为AD的中点,以CE为折痕把△DEC折起,使点D到达点P的位置,且点P的射影O落在线段AC上.
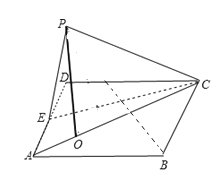
(1)求![]() ;
;
(2)求几何体P﹣ABCE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com