
【题目】在数列{an}中, ![]() (c为常数,n∈N*),且a1 , a2 , a5成公比不为1的等比数列. (Ⅰ)求证:数列
(c为常数,n∈N*),且a1 , a2 , a5成公比不为1的等比数列. (Ⅰ)求证:数列 ![]() 是等差数列;
是等差数列;
(Ⅱ)求c的值;
(Ⅲ)设bn=anan+1 , 求数列{bn}的前n项和Sn .
【答案】解:(Ⅰ)因为 ![]() ,所以an≠0, 则
,所以an≠0, 则 ![]() ,又c为常数,
,又c为常数,
∴数列 ![]() 是等差数列;
是等差数列;
(Ⅱ)由(Ⅰ)可知 ![]() ,
,
∵a1=1,∴a2= ![]() ,a5=
,a5= ![]() ,
,
∵a1 , a2 , a5成公比不为1的等比数列,所以 ![]() ,
,
解得c=0或c=2,当c=0时,an=an+1 , 不满足题意,舍去,
所以c的值为2;
(Ⅲ)由(Ⅱ)可知c=2,∴ ![]() ,
,
bn=anan+1= ![]() =
= ![]() ,
,
所以数列{bn}的前n项和
Sn= ![]() =
= ![]()
【解析】(Ⅰ)通过已知条件,方程去倒数,即可推出数列满足等差数列的定义,说明数列 ![]() 是等差数列;(Ⅱ)通过第一问,直接求出a1 , a2 , a5 , 利用等比数列直接求出c的值;(Ⅲ)通过第二问,求出an , 然后利用bn=anan+1 , 通过裂项法直接求数列{bn}的前n项和Sn .
是等差数列;(Ⅱ)通过第一问,直接求出a1 , a2 , a5 , 利用等比数列直接求出c的值;(Ⅲ)通过第二问,求出an , 然后利用bn=anan+1 , 通过裂项法直接求数列{bn}的前n项和Sn .
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系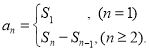 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣2|x﹣1|. (Ⅰ)求不等式f(x)≥﹣2的解集M;
(Ⅱ)对任意x∈[a,+∞),都有f(x)≤x﹣a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求: (Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,但取球次数最多不超过4次,求取球次数ξ的概率分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
A.21
B.20
C.19
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D(x0 , y0)为圆O:x2+y2=12上一点,E(x0 , 0),动点P满足 ![]() =
= ![]() +
+ ![]() ,设动点P的轨迹为曲线C.
,设动点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)若动直线l:y=kx+m与曲线C相切,过点A1(﹣2,0),A2(2,0)分别作A1M⊥l于M,A2N⊥l于N,垂足分别是M,N,问四边形A1MNA2的面积是否存在最值?若存在,请求出最值及此时k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的图象如图所示,为了得到g(x)=cos2x的图象,则只需将f(x)的图象( )
的图象如图所示,为了得到g(x)=cos2x的图象,则只需将f(x)的图象( ) 
A.向右平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,已知点P(0, ![]() ),曲线C的参数方程为
),曲线C的参数方程为 ![]() (φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=
(φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ= ![]() .
.
(Ⅰ)判断点P与直线l的位置关系并说明理由;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com