
°æƒø°øƒ≥∆∑≈∆µÁ ”…˙≤˙≥ߺ“”–A£¨B¡Ω÷÷–Õ∫≈µƒµÁ ”ª˙≤Œº”¡Àº“µÁœ¬œÁªÓ∂Ø£¨»Ù≥ߺ“∂‘A£¨B¡Ω÷÷–Õ∫≈µƒµÁ ”ª˙µƒÕ∂∑≈Ω∂Ó∑÷±Œ™p£¨qÕÚ‘™£¨≈©√Òπ∫¬ÚµÁ ”ª˙ªÒµ√µƒ≤πÃ˘∑÷±Œ™![]() p£¨
p£¨ ![]() ln qÕÚ‘™£¨“—÷™A£¨B¡Ω÷÷–Õ∫≈µƒµÁ ”ª˙µƒÕ∂∑≈◊Ð∂ÓŒ™10ÕÚ‘™£¨«“A£¨B¡Ω÷÷–Õ∫≈µƒµÁ ”ª˙µƒÕ∂∑≈Ω∂Óæ˘≤ªµÕ”⁄1ÕÚ‘™£¨«Îƒ„÷∆∂®“ª∏ˆÕ∂∑≈∑Ω∞∏£¨ πµ√‘⁄’‚¥ŒªÓ∂Ø÷–≈©√Òµ√µΩµƒ≤πÃ˘◊Ó∂ý£¨≤¢«Û≥ˆ◊Ó¥Û÷µ£Æ(æ´»∑µΩ0.1£¨≤Œøº ˝æð£∫ln 4°÷1.4)
ln qÕÚ‘™£¨“—÷™A£¨B¡Ω÷÷–Õ∫≈µƒµÁ ”ª˙µƒÕ∂∑≈◊Ð∂ÓŒ™10ÕÚ‘™£¨«“A£¨B¡Ω÷÷–Õ∫≈µƒµÁ ”ª˙µƒÕ∂∑≈Ω∂Óæ˘≤ªµÕ”⁄1ÕÚ‘™£¨«Îƒ„÷∆∂®“ª∏ˆÕ∂∑≈∑Ω∞∏£¨ πµ√‘⁄’‚¥ŒªÓ∂Ø÷–≈©√Òµ√µΩµƒ≤πÃ˘◊Ó∂ý£¨≤¢«Û≥ˆ◊Ó¥Û÷µ£Æ(æ´»∑µΩ0.1£¨≤Œøº ˝æð£∫ln 4°÷1.4)
°æ¥∞∏°ø≥ߺ“∂‘A£¨B¡Ω÷÷–Õ∫≈µƒµÁ ”ª˙µƒÕ∂∑≈Ω∂Ó∑÷±Œ™6ÕÚ‘™∫Õ4ÕÚ‘™ ±£¨≈©√Òµ√µΩµƒ≤πÃ˘◊Ó∂ý£¨◊Ó∂ý≤πÃ˘‘º1.2ÕÚ‘™£Æ
°æΩ‚Œˆ°ø’‚ «¿˚”√µº ˝—–æø”≈ªØŒ µƒµ‰¿˝Ã‚ƒø£¨œ»«Û≥ˆ≤πÃ˘y”ÎB–Õ∫≈µÁ ”ª˙µƒÕ∂∑≈Ω∂ÓxÕÚ‘™÷ƺ‰µƒ∫Ø ˝πÿœµ Ω.»ª∫Û¿˚”√µº ˝«Û◊Ó÷µº¥ø….◊¢“‚”¶”√“ª∞„∂º «µ•∑Â∫Ø ˝£¨µº ˝µ»”⁄¡„µƒµ„“ª∞„æÕ «“™«Û»°◊Ó¥Û÷µ ±xµƒ÷µ


 √˚–£√˚ ¶≈ý”≈◊˜“µ±æº”∫À–ƒ ‘æÌœµ¡–¥∞∏
√˚–£√˚ ¶≈ý”≈◊˜“µ±æº”∫À–ƒ ‘æÌœµ¡–¥∞∏ »´≥ÃΩæÌœµ¡–¥∞∏
»´≥ÃΩæÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥÷–—ß∏þ»˝ƒÍº∂¥”º◊°¢““¡Ω∏ˆ∞ýº∂∏˜—°≥ˆ7√˚—ß…˙≤Œº” ˝—ßæ∫»¸£¨À˚√«»°µ√µƒ≥…º®£®¬˙∑÷100∑÷£©µƒæ•“∂Õº»ÁÕº£¨∆‰÷–º◊∞ý—ß…˙µƒ∆Ωæ˘∑÷ «85£¨““∞ý—ß…˙≥…º®µƒ÷–Œª ˝ «83£¨‘Úx+yµƒ÷µŒ™ £Æ 
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™√¸Ã‚p£∫≤ªµ» Ω(m£≠1)x2£´(m£≠1)x£´2>0µƒΩ‚ºØ «R£¨√¸Ã‚q£∫sin x£´cos x>m.»Áπ˚∂‘”⁄»Œ“‚µƒx° R£¨√¸Ã‚p «’Ê√¸Ã‚«“√¸Ã‚qŒ™ºŸ√¸Ã‚£¨«Ûmµƒ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝Àƒ√ÊÃÂ![]() µƒ∂•µ„
µƒ∂•µ„![]() ∑÷±‘⁄¡Ω¡Ω¥π÷±µƒ»˝Ãı…‰œþ
∑÷±‘⁄¡Ω¡Ω¥π÷±µƒ»˝Ãı…‰œþ![]() …œ£¨‘⁄œ¬¡–√¸Ã‚÷–£¨¥ÌŒÛµƒ «£® £©
…œ£¨‘⁄œ¬¡–√¸Ã‚÷–£¨¥ÌŒÛµƒ «£® £©

A. Àƒ√ÊÃÂ![]() «’˝»˝¿‚◊∂ B. ÷±œþ
«’˝»˝¿‚◊∂ B. ÷±œþ![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() œýΩª C. “Ï√Ê÷±œþ
œýΩª C. “Ï√Ê÷±œþ![]() ∫Õ
∫Õ![]() À˘≥…Ω« «
À˘≥…Ω« «![]() D. ÷±œþ
D. ÷±œþ![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…µƒΩ«µƒ’˝œ“÷µŒ™
À˘≥…µƒΩ«µƒ’˝œ“÷µŒ™![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“‘÷±Ω«◊¯±Íœµµƒ‘≠µ„![]() Œ™º´µ„£¨
Œ™º´µ„£¨ ![]() ÷·’˝∞Î÷·Œ™º´÷·£¨≤¢‘⁄¡Ω÷÷◊¯±Íœµ÷–»°œýÕ¨µƒ≥§∂»µ•Œª£¨“—÷™÷±œþ
÷·’˝∞Î÷·Œ™º´÷·£¨≤¢‘⁄¡Ω÷÷◊¯±Íœµ÷–»°œýÕ¨µƒ≥§∂»µ•Œª£¨“—÷™÷±œþ![]() µƒ≤Œ ˝∑Ω≥ÃŒ™
µƒ≤Œ ˝∑Ω≥ÃŒ™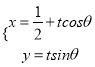 £¨£®
£¨£® ![]() Œ™≤Œ ˝£¨
Œ™≤Œ ˝£¨ ![]() £©£¨«˙œþ
£©£¨«˙œþ![]() µƒº´◊¯±Í∑Ω≥ÃŒ™
µƒº´◊¯±Í∑Ω≥ÃŒ™![]() .
.
£®1£©«Û«˙œþ![]() µƒ÷±Ω«◊¯±Í∑Ω≥ãª
µƒ÷±Ω«◊¯±Í∑Ω≥ãª
£®2£©…Ë÷±œþ![]() ”Ϋ˙œþ
”Ϋ˙œþ![]() œýΩª”⁄
œýΩª”⁄![]() £¨
£¨ ![]() ¡Ωµ„£¨µ±
¡Ωµ„£¨µ±![]() ±‰ªØ ±£¨«Û
±‰ªØ ±£¨«Û![]() µƒ◊Ó–°÷µ.
µƒ◊Ó–°÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄°˜ABC÷–£¨Ω«A£¨B£¨CÀ˘∂‘µƒ±þ≥§∑÷±Œ™a£¨b£¨c£¨B= ![]() £Æ
£Æ
£®1£©»Ùa=3£¨b= ![]() £¨«Ûcµƒ÷µ£ª
£¨«Ûcµƒ÷µ£ª
£®2£©»Ùf£®A£©=sinA£® ![]() cosA©ÅsinA£©£¨a=
cosA©ÅsinA£©£¨a= ![]() £¨«Ûf£®A£©µƒ◊Ó¥Û÷µº∞¥À ±°˜ABCµƒÕ‚Ω”‘≤∞Îæ∂£Æ
£¨«Ûf£®A£©µƒ◊Ó¥Û÷µº∞¥À ±°˜ABCµƒÕ‚Ω”‘≤∞Îæ∂£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø(2013°§∫˛±±∏þøº)Àƒ√˚Õ¨—ß∏˘æð∏˜◊‘µƒ—˘±æ ˝æð—–æø±‰¡øx£¨y÷ƺ‰µƒœýπÿπÿœµ£¨≤¢«Ûµ√ªÿπÈ÷±œþ∑Ω≥ã¨∑÷±µ√µΩ“‘œ¬Àƒ∏ˆΩ·¬€£∫
¢Ÿy”Îx∏∫œýπÿ«“![]() £Ω2.347x£≠6.423£ª
£Ω2.347x£≠6.423£ª
¢⁄y”Îx∏∫œýπÿ«“![]() £Ω£≠3.476x£´5.648£ª
£Ω£≠3.476x£´5.648£ª
¢€y”Îx’˝œýπÿ«“![]() £Ω5.437x£´8.493£ª
£Ω5.437x£´8.493£ª
¢Ðy”Îx’˝œýπÿ«“![]() £Ω£≠4.326x£≠4.578.
£Ω£≠4.326x£≠4.578.
∆‰÷–“ª∂®≤ª’˝»∑µƒΩ·¬€µƒ–Ú∫≈ «( )
A. ¢Ÿ¢⁄ B. ¢⁄¢€ C. ¢€¢Ð D. ¢Ÿ¢Ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂´ð∏ –ƒ≥∏þº∂÷–—ß‘⁄ΩÒƒÍ4‘¬∑ð∞≤◊∞¡À“ª≈˙ø’µ˜£¨πÿ”⁄’‚≈˙ø’µ˜µƒ π”√ƒÍœÞ
![]() £®µ•Œª£∫ƒÍ£¨
£®µ•Œª£∫ƒÍ£¨ ![]() £©∫ÕÀ˘÷ß≥ˆµƒŒ¨ª§∑—”√
£©∫ÕÀ˘÷ß≥ˆµƒŒ¨ª§∑—”√![]() £®µ•Œª£∫ÕÚ‘™£©≥ߺ“Ã·π©µƒÕ≥º∆◊ ¡œ»Áœ¬£∫
£®µ•Œª£∫ÕÚ‘™£©≥ߺ“Ã·π©µƒÕ≥º∆◊ ¡œ»Áœ¬£∫
π”√ƒÍœÞ | 1 | 2 | 3 | 4 | 5 |
Œ¨ª§∑—”√ | 6 | 7 | 7.5 | 8 | 9 |
![]() «Î∏˘æð“‘…œ ˝æ𣨔√◊Ó–°∂˛≥À∑®‘≠¿Ì«Û≥ˆŒ¨ª§∑—”√
«Î∏˘æð“‘…œ ˝æ𣨔√◊Ó–°∂˛≥À∑®‘≠¿Ì«Û≥ˆŒ¨ª§∑—”√![]() πÿ”⁄
πÿ”⁄![]() µƒœþ–‘ªÿπÈ∑Ω≥Ã
µƒœþ–‘ªÿπÈ∑Ω≥Ã![]() £ª
£ª
![]() »ÙπÊ∂®µ±Œ¨ª§∑—”√
»ÙπÊ∂®µ±Œ¨ª§∑—”√![]() ≥¨π˝13.1ÕÚ‘™ ±£¨∏√≈˙ø’µ˜±ÿ–α®∑œ£¨ ‘∏˘æð£®1£©µƒΩ·¬€«Û∏√≈˙ø’µ˜ π”√ƒÍœÞµƒ◊Ó¥Û÷µ.
≥¨π˝13.1ÕÚ‘™ ±£¨∏√≈˙ø’µ˜±ÿ–α®∑œ£¨ ‘∏˘æð£®1£©µƒΩ·¬€«Û∏√≈˙ø’µ˜ π”√ƒÍœÞµƒ◊Ó¥Û÷µ.
≤Œøºπ´ Ω£∫◊Ó–°∂˛≥Àπ¿º∆œþ–‘ªÿπÈ∑Ω≥Ã![]() ÷–œµ ˝º∆À„π´ Ω£∫
÷–œµ ˝º∆À„π´ Ω£∫
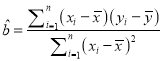 £¨
£¨ ![]() £¨
£¨ ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
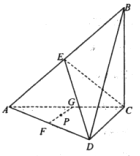
°æƒø°ø»ÁÕº£¨‘⁄Àƒ√ÊÃÂ![]() ÷–£¨∆Ω√Ê
÷–£¨∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() ∑÷±Œ™
∑÷±Œ™![]() £¨
£¨ ![]() £¨
£¨ ![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨ ![]() £¨
£¨ ![]() .
.
£®1£©«Û÷§£∫ ![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©»Ù![]() Œ™
Œ™![]() …œ»Œ“ªµ„£¨÷§√˜
…œ»Œ“ªµ„£¨÷§√˜![]() ∆Ω√Ê
∆Ω√Ê![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com