
【题目】杭州西溪国家湿地公园是以水为主题的公园,以湿地良好生态环境和多样化湿地景观资源为基础的生态型主题公园.欲在该公园内搭建一个平面凸四边形![]() 的休闲观光及科普宣教的平台,如图所示,其中
的休闲观光及科普宣教的平台,如图所示,其中![]() 百米,
百米,![]() 百米,
百米,![]() 为正三角形.建成后
为正三角形.建成后![]() 将作为人们旅游观光休闲娱乐的区域,
将作为人们旅游观光休闲娱乐的区域,![]() 将作为科普宣教湿地功能利用弘扬湿地文化的区域.
将作为科普宣教湿地功能利用弘扬湿地文化的区域.
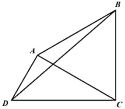
(1)当![]() 时,求旅游观光休闲娱乐的区域
时,求旅游观光休闲娱乐的区域![]() 的面积;
的面积;
(2)求旅游观光休闲娱乐的区域![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)![]() 通过余弦定理可求得
通过余弦定理可求得![]() ,进而得到
,进而得到![]() ,
,![]() ,
,![]() ,根据直角三角形的面积公式即可求得结果.
,根据直角三角形的面积公式即可求得结果.
(2)方法一:设![]() ,由余弦定理可求得
,由余弦定理可求得![]() ,设
,设![]() ,进而由余弦定理可得
,进而由余弦定理可得![]() ,则可求
,则可求![]() 的值, 进而可得
的值, 进而可得![]() 的值,根据面积公式化简可得
的值,根据面积公式化简可得![]() ,令
,令![]() ,则面积可化简为
,则面积可化简为![]() ,令
,令![]() ,平方后化简为
,平方后化简为![]() 由
由![]() 的存在性可知
的存在性可知![]() 即可求得
即可求得![]() ,进而得出结果.
,进而得出结果.
方法二: 不妨设![]() ,
,![]() ,由正余弦定理可得
,由正余弦定理可得![]() ,
,
![]() ,
,![]()
利用面积公式及辅助角公式化简![]() 根据三角函数性质即可得出结果.
根据三角函数性质即可得出结果.
方法三:设![]() ,
,![]() ,由余弦定理可知
,由余弦定理可知
![]() ,
,![]() 为正三角形及由正弦定理得可得
为正三角形及由正弦定理得可得![]() ,
,![]() 由
由![]() 代入化简可得
代入化简可得![]() 根据面积公式及辅助角公式化简可得
根据面积公式及辅助角公式化简可得![]() ,由三角函数性质即可得出结果.
,由三角函数性质即可得出结果.
法一:(1)∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]() ,
,![]()
∵![]() 为正
为正![]() ,∴
,∴![]() ,
,![]()
∴![]() ,∴
,∴![]()
(2)设![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
设![]() ,∴
,∴![]() ,
,![]() ,
,![]()
∴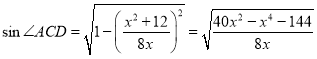
∴![]()
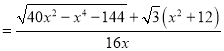
∴
令![]() ,∴上式
,∴上式![]()
令![]() ,∴
,∴![]()
∴![]() ,
,![]()
∴![]()
法二:(1)![]() ,∴
,∴![]()
又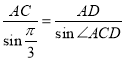 ,∴
,∴![]() ,∴
,∴![]()
![]()
(2)不妨设![]() ,
,![]()
于是![]() ①
①
![]() ②
②
![]() ③
③
∴
![]()
当且仅当![]() 时,∴
时,∴![]() 面积最大为
面积最大为![]()
法三:(1)由![]() 中,
中,![]() ,
,![]() ,
,![]()
则由余弦定理c![]() ,∴
,∴![]()
又![]() 为正三角形,∴
为正三角形,∴![]()
∴![]()
(2)在![]() 中,设∠
中,设∠![]() ,
,![]()
由余弦定理得![]()
∵![]() 为正三角形,∴
为正三角形,∴![]()
由正弦定理得![]() ,即
,即![]()
∴![]() ,∴
,∴![]() (*)
(*)
∵![]()
又由![]() ,∴
,∴![]() ,∴
,∴![]() 为锐角,∴
为锐角,∴![]() (**)
(**)
∴![]()
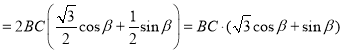
(由*和**)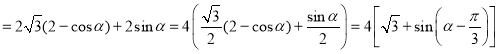
∴当![]() ,即当
,即当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
∴![]() 面积最大值为
面积最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
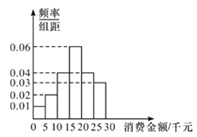
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”;
列联表,并判断有多大把握认为“网购迷与性别有关系”;
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 | 100 |
(3)调査显示,甲、乙两人每次网购采用的支付方式相互独立,两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式,所得数据如下表所示:
网购总次数 | 支付宝支付次数 | 银行卡支付次数 | 微信支付次数 | |
甲 | 80 | 40 | 16 | 24 |
乙 | 90 | 60 | 18 | 12 |
将频率视为概率,若甲、乙两人在下周内各自网购2次,记两人采用支付宝支付的次数之和为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:观测值公式: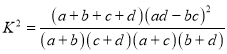
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axex,g(x)=x2+2x+b,若曲线y=f(x)与曲线y=g(x)都过点P(1,c).且在点P处有相同的切线l.
(Ⅰ)求切线l的方程;
(Ⅱ)若关于x的不等式k[ef(x)]≥g(x)对任意x∈[﹣1,+∞)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,直线
,直线![]() 过椭圆的
过椭圆的![]() 左焦点.
左焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 的平分线在
的平分线在![]() 轴上,
轴上,![]() .试判断直线
.试判断直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在a>0,使得函数f(x)=6a2lnx+4ax与g(x)=x2﹣b在这两函数图象的公共点处的切线相同,则b的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)当a![]() 0,b
0,b![]() 0时,若F(x)
0时,若F(x)![]() f(x)+g(x)的值域为[5,+∞),求证:
f(x)+g(x)的值域为[5,+∞),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 上一点
上一点![]() 处的切线
处的切线![]() 分别交
分别交![]() 轴
轴![]() 轴于点
轴于点![]() ,以
,以![]() 为顶点且以
为顶点且以![]() 为中心的椭圆记作
为中心的椭圆记作![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点.
两点.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求
,求![]() 点坐标;
点坐标;
(2)证明:四边形![]() 的面积
的面积![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com