
【题目】下列结论:
![]() “直线l与平面
“直线l与平面![]() 平行”是“直线l在平面
平行”是“直线l在平面![]() 外”的充分不必要条件;
外”的充分不必要条件;
![]() 若p:
若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]() ;
;
![]() 命题“设a,
命题“设a,![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”为真命题;
”为真命题;
![]() “
“![]() ”是“函数
”是“函数![]() 在
在![]() 上单调递增”的充要条件.
上单调递增”的充要条件.
其中所有正确结论的序号为______.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,
,![]() .
.
(1)直线![]() 是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
(2)已知点![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 满足条件
满足条件![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由一平面内的
是由一平面内的![]() 个向量组成的集合.若
个向量组成的集合.若![]() ,且
,且![]() 的模不小于
的模不小于![]() 中除
中除![]() 外的所有向量和的模.则称
外的所有向量和的模.则称![]() 是
是![]() 的极大向量.有下列命题:
的极大向量.有下列命题:
①若![]() 中每个向量的方向都相同,则
中每个向量的方向都相同,则![]() 中必存在一个极大向量;
中必存在一个极大向量;
②给定平面内两个不共线向量![]() ,在该平面内总存在唯一的平面向量
,在该平面内总存在唯一的平面向量![]() ,使得
,使得![]() 中的每个元素都是极大向量;
中的每个元素都是极大向量;
③若![]() 中的每个元素都是极大向量,且
中的每个元素都是极大向量,且![]() 中无公共元素,则
中无公共元素,则![]() 中的每一个元素也都是极大向量.
中的每一个元素也都是极大向量.
其中真命题的序号是_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抢“微信红包”已经成为中国百姓欢度春节时非常喜爱的一项活动.小明收集班内20名同学今年春节期间抢到红包金额![]() (元)如下(四舍五入取整数):
(元)如下(四舍五入取整数):
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
对这20个数据进行分组,各组的频数如下:

(Ⅰ)写出m,n的值,并回答这20名同学抢到的红包金额的中位数落在哪个组别;
(Ⅱ)记C组红包金额的平均数与方差分别为![]() 、
、![]() ,E组红包金额的平均数与方差分别为
,E组红包金额的平均数与方差分别为![]() 、
、![]() ,试分别比较
,试分别比较![]() 与
与![]() 、
、![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从A,E两组所有数据中任取2个,求这2个数据差的绝对值大于100的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限![]() 和所支出的维修费用
和所支出的维修费用![]() (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知![]() 对
对![]() 呈线性相关关系.
呈线性相关关系.
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程![]() 的回归系数
的回归系数![]() .
.
(3)估计使用年限为10年时,维修费用是多少?
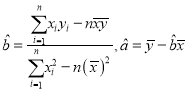
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com