
【题目】俗话说“三个臭皮匠,顶个诸葛亮”,从数学角度解释这句话的含义.
【答案】见解析.
【解析】
转化为三个臭皮匠解决一个问题的概率要大于诸葛壳解决这个问题的概率.利用对立事件的概率公式和相互独立事件的乘法公式可得结论.
解:“三个臭皮匠,顶个诸葛亮”比喻人多智慧多,有事情经过大家商量,就能商量出一个好办法来,从数学角度来理解,即三个臭皮匠解决一个问题的概率要大于诸葛壳解决这个问题的概率.
例如,假设诸葛亮解出问题的概率为0.8,臭皮匠老大解出问题的概率为0.5,老二为0.45,老三为0.4,且每个人独立解题,则三个臭皮匠中至少有一人解出问题的概率一定大于诸葛亮解出问题的概率.
不妨设“臭皮匠老大解出问题”为事件A,“老二解出问题”为事件B,“老三解出问题”为事件C,“诸葛亮解出问题”为事件D.
于是三个臭皮匠中至少有一人解出问题的概率为![]() ,所以合三个臭皮匠之力解出问题的概率大过诸葛亮解出这个问题的概率.
,所以合三个臭皮匠之力解出问题的概率大过诸葛亮解出这个问题的概率.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资![]() (单位:元)与月销售产品件数
(单位:元)与月销售产品件数![]() 的函数关系式;
的函数关系式;
(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数 | 300 | 400 | 500 | 600 | 700 |
次数 | 2 | 4 | 9 | 5 | 4 |
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() 为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
(Ⅰ)现从抽取的6件合格产品中再任选3件,求恰好取到2件优等品的概率;
(Ⅱ)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(i)根据所给统计量,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(ii)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系
的关系![]() ,则当优等品的尺寸为
,则当优等品的尺寸为![]() 为何值时,收益
为何值时,收益![]() 的预报值最大?(精确到0.1)
的预报值最大?(精确到0.1)
附:对于样本![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数有_________
(1)已知变量![]() 和
和![]() 满足关系
满足关系![]() ,则
,则![]() 与
与![]() 正相关;(2)线性回归直线必过点
正相关;(2)线性回归直线必过点![]() ;
;
(3)对于分类变量![]() 与
与![]() 的随机变量
的随机变量![]() ,
,![]() 越大说明“
越大说明“![]() 与
与![]() 有关系”的可信度越大
有关系”的可信度越大
(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数![]() 的值越大,说明拟合的效果越好.
的值越大,说明拟合的效果越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 距离之和的最小值为( )
距离之和的最小值为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.函数 在区间
在区间![]() 上有且只有
上有且只有![]() 个零点
个零点
B.若函数![]() ,则
,则![]()
C.如果函数![]() 在
在![]() 上单调递增,那么它在
上单调递增,那么它在![]() 上单调递减
上单调递减
D.若函数![]() 的图象关于点
的图象关于点![]() 对称,则函数
对称,则函数![]() 为奇函数
为奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,如图.
,如图.
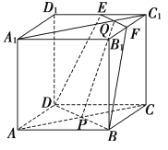
(1)若![]() 交平面
交平面![]() 于点
于点![]() ,证明:
,证明:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,若存在确定
,若存在确定![]() 的位置,若不存在说明理由.
的位置,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com