
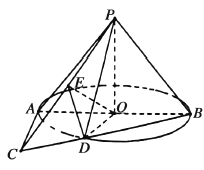
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.
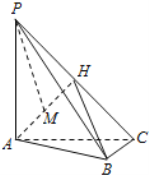
(Ⅰ)求证:AH⊥平面PBC;
(Ⅱ)求PM与平面AHB成角的正弦值;
(Ⅲ)在线段PB上是否存在点N,使得MN∥平面ABC,若存在,请说明点N的位置,若不存在,请说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)![]() (Ⅲ)点N是靠近B点的四等分点
(Ⅲ)点N是靠近B点的四等分点
【解析】
(Ⅰ)根据线面垂直判定与性质定理进行论证,(Ⅱ)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得平面AHB的一个法向量,根据向量数量积求向量夹角,最后根据向量夹角与线面角关系得结果,(Ⅲ)先设N坐标,再根据![]() 与平面ABC的法向量的数量积为零解得结果.
与平面ABC的法向量的数量积为零解得结果.
(Ⅰ)证明:∵PA⊥底面ABC,
∴PA⊥BC,
又∵AC⊥BC,PA∩AC=A,
∴BC⊥平面PAC,
∵AH平面PAC,
∴BC⊥AH.
∵H为PC的中点,PA=AC,
∴AH⊥PC.
∵PC∩BC=C.
∴AH⊥平面PBC;
(Ⅱ)
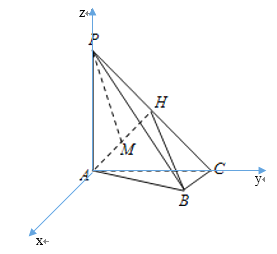
由题意建立空间直角坐标系.A(0,0,0),B(1,2,0),C(0,2,0),
P(0,0,2),H(0,1,1),M![]() .
.
![]() =(0,1,1),
=(0,1,1),![]() =(1,2,0),
=(1,2,0),![]() =
=![]() .
.
设平面ABH的法向量为![]() =(x,y,z),则
=(x,y,z),则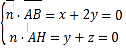 ,取
,取![]() =(2,-1,1).
=(2,-1,1).
设PM与平面AHB成角为![]() ,
,
则sin![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
所以PM与平面AHB成角的正弦值为![]()
(Ⅲ)假设在线段PB上存在点N,使得MN∥平面ABC.
设![]() ,
,![]() =(1,2,-2),
=(1,2,-2),
∴![]() .
.
∴![]() =
=![]() =
=![]() ,
,
∵MN∥平面ABC,平面ABC的法向量为![]() =(0,0,2),
=(0,0,2),
∴![]() =
=![]() -
-![]() =0,解得
=0,解得![]() .
.
∴点N是靠近B点的四等分点.


科目:高中数学 来源: 题型:
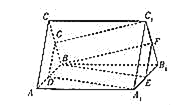
【题目】如图所示,三棱柱ABC﹣A1B1C1的侧棱垂直于底面,且底面是边长为2的正三角形,AA1=3,点D,E,F,G分别是所在棱的中点.
(Ⅰ)证明:平面BEF∥平面DA1C1;
(Ⅱ)求三棱柱ABC﹣A1B1C1夹在平面BEF和平面DA1C1之间的部分的体积.
附:台体的体积![]() ,其中S和S′分别是上、下底面面积,h是台体的高.
,其中S和S′分别是上、下底面面积,h是台体的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
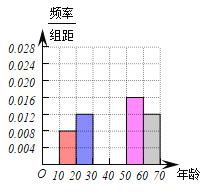
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月20日,重庆市实施高考改革方案,2018年秋季入学的高中一年级的学生将实行“![]() ”模式.即“3”为全国统考科目语文、数学、外语所有学生必考;“1”为物理、历史科目中选择一科俗称“2选1”;“2”为再选学科,考生可在化学、生物、思想政治、地理4个科目中选择两科俗称“4选2”,选择学科完全相同即为相同“组合”.某校高一年级有三名同学甲,乙,丙根据自己喜欢的大学和专业情况均选择了物理,为了了解“4选2”选科情况老师找这三名同学来谈话情况如下:
”模式.即“3”为全国统考科目语文、数学、外语所有学生必考;“1”为物理、历史科目中选择一科俗称“2选1”;“2”为再选学科,考生可在化学、生物、思想政治、地理4个科目中选择两科俗称“4选2”,选择学科完全相同即为相同“组合”.某校高一年级有三名同学甲,乙,丙根据自己喜欢的大学和专业情况均选择了物理,为了了解“4选2”选科情况老师找这三名同学来谈话情况如下:
甲说:我选了化学,但没有选思想政治;
乙说:我与甲有一科相同,但没有选化学和地理;
丙说:我与甲有相同的选科,与乙也有相同选科,但我们三个选的“组合”都不相同.则下列结论正确的是( )
A.甲选了化学和地理B.丙可能选化学和思想政治
C.甲一定选地理D.丙一定选了生物和地理
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,
,![]() 为椭圆上任意一点,
为椭圆上任意一点,![]() 的最大面积为
的最大面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,若
,若![]() 的内切圆面积为
的内切圆面积为![]() ,则求直线
,则求直线![]() 方程.
方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 为顶点,母线长为
为顶点,母线长为![]() 的圆锥中,底面圆
的圆锥中,底面圆![]() 的直径
的直径![]() 长为2,
长为2,![]() 是圆
是圆![]() 所在平面内一点,且
所在平面内一点,且![]() 是圆
是圆![]() 的切线,连接
的切线,连接![]() 交圆
交圆![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,当二面角
,当二面角![]() 的大小为
的大小为![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com