
 的图象关于直线
的图象关于直线 对称,那么a等于( )
对称,那么a等于( )A. | B.- | C.1 | D.-1 |
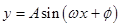 的对称轴一定经过图象的波峰顶或波谷底,且与y轴平行,而对称中心是图象与x轴的交点,学生对函数的对称性不理解误认为当
的对称轴一定经过图象的波峰顶或波谷底,且与y轴平行,而对称中心是图象与x轴的交点,学生对函数的对称性不理解误认为当 时,y=0,导致解答出错。
时,y=0,导致解答出错。 ,故
,故 的最大值为
的最大值为 ,依题意,直线
,依题意,直线 是函数的对称轴,则它通过函数的最大值或最小值点即
是函数的对称轴,则它通过函数的最大值或最小值点即
 ,解得
,解得 .故选D
.故选D ,直线
,直线 是函数的对称轴,故有
是函数的对称轴,故有 ,即:
,即: ,而
,而
 ,从而
,从而 故选D.
故选D. 是函数的对称则必有
是函数的对称则必有 ,代入即得
,代入即得 。挂选D。
。挂选D。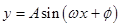 及余弦型函数
及余弦型函数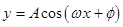 它们有无穷多条对称轴及无数多个对称中心,它们的意义是分别使得函数取得最值的x值和使得函数值为零的x值,这是它们的几何和代数特征。希望同学们认真学习本题的三种解法根据具体问题的不同灵活处理。
它们有无穷多条对称轴及无数多个对称中心,它们的意义是分别使得函数取得最值的x值和使得函数值为零的x值,这是它们的几何和代数特征。希望同学们认真学习本题的三种解法根据具体问题的不同灵活处理。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com