
【题目】已知抛物线![]() ,过
,过![]() 的直线与抛物线
的直线与抛物线![]() 相交于
相交于![]() 两点.
两点.
(1)若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(2)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为平面上一点,
为平面上一点,![]() 为直线
为直线![]() :
:![]() 上任意一点,过点
上任意一点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,设线段
,设线段![]() 的中垂线与直线
的中垂线与直线![]() 交于点
交于点![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的直线
作互相垂直的直线![]() 与
与![]() ,其中直线
,其中直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,设点
,设点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,求
的中点,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF中,AB=![]() ,CE=1,CE⊥平面ABCD.
,CE=1,CE⊥平面ABCD.
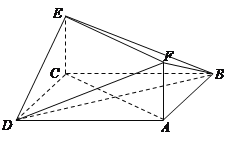
(1)求异面直线DF与BE所成角的余弦值;
(2)求二面角A-DF-B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“家校连心,立德树人——重温爱国故事,弘扬爱国主义精神社会课堂”活动中,王老师组建了一个微信群,群的成员由学生、家长、老师和讲解员共同组成.已知该微信群中男学生人数多于女生人数,女学生人数多于家长人数,家长人数多于教师人数,教师人数多于讲解员人数,讲解员人数的两倍多于男生人数.若把这5类人群的人数作为一组数据,当该微信群总人数取最小值时,这组数据的中位数是( )
A.5B.6C.7D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在圆
在圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 上的点
上的点![]() 满足
满足![]() .过点
.过点![]() 作直线
作直线![]() 垂直于线段
垂直于线段![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)证明:![]() 恒过定点;
恒过定点;
(ⅱ)设线段![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com