
某地开发了一个旅游景点,第1年的游客约为100万人,第2年的游客约为120万人.某数学兴趣小组综合各种因素预测:①该景点每年的游客人数会逐年增加;②该景点每年的游客都达不到130万人.该兴趣小组想找一个函数 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系.
(1)根据上述两点预测,请用数学语言描述函数 所具有的性质;
所具有的性质;
(2)若 =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测;
(3)若 =
= ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围.
(1)详见解析;(2)详见解析;(3)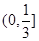 .
.
解析试题分析:(1)易知函数在定义域上是增函数,函数值不大于130;(2)把前两年的数据即(1,100),(2,120)代入函数的解析式,解关于 的方程组即可求出
的方程组即可求出 的值,再考查所得的函数是否具有(1)中的两条性质;(3)由(1,100),(2,120)两组数据,可得到
的值,再考查所得的函数是否具有(1)中的两条性质;(3)由(1,100),(2,120)两组数据,可得到 的两个关系式,用
的两个关系式,用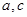 表示
表示 ,问题就转化为一个含有参数
,问题就转化为一个含有参数 的函数具备两条性质,求参数取值范围的问题,可用导数知识和解决不等式恒成立问题的一般方法解决.
的函数具备两条性质,求参数取值范围的问题,可用导数知识和解决不等式恒成立问题的一般方法解决.
试题解析:(1)预测①: 在
在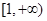 上单调递增;
上单调递增;
预测②: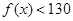 对
对 恒成立; 2分
恒成立; 2分
(2)将(1,100)、(2、120)代入到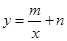 中,得
中,得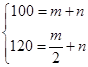 ,解得
,解得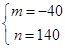 .
.
5分
因为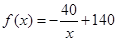 ,所以
,所以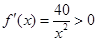 ,
,
故 在
在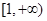 上单调递增,符合预测①; 7分
上单调递增,符合预测①; 7分
又当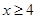 时,
时,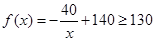 ,所以此时
,所以此时 不符合预测②. 9分
不符合预测②. 9分
(3)由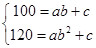 ,解得
,解得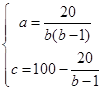 . 11分
. 11分
因为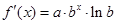 ,要想符合预测①,则
,要想符合预测①,则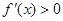 ,
,
即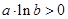 ,从而
,从而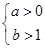 或
或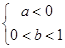 . 12分
. 12分
[1]当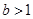 时,
时,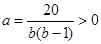 ,此时符合预测①,但由
,此时符合预测①,但由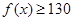 ,解得
,解得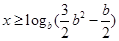 ,
,
即当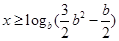 时,
时,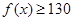 ,所以此时
,所以此时 不符合预测②;13分
不符合预测②;13分
[2]当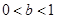 ,
,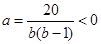 ,此时符合预测①,又由
,此时符合预测①,又由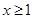 ,知
,知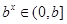 ,所以
,所以 ,从而
,从而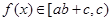 .
.
欲 也符合预测②,则
也符合预测②,则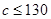 ,即
,即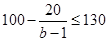 ,又
,又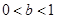 ,解得
,解得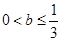 .
.
综上所述, 的取值范围是
的取值范围是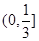 . 16分
. 16分
考点:函数在实际问题中的应用,导数的应用.


科目:高中数学 来源: 题型:解答题
已知偶函数 满足:当
满足:当 时,
时, ,当
,当 时,
时, .
.
(Ⅰ).求 表达式;
表达式;
(Ⅱ).若直线 与函数
与函数 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数 的取值范围;
的取值范围;
(Ⅲ).试讨论当实数 满足什么条件时,直线
满足什么条件时,直线 的图像恰有
的图像恰有 个公共点
个公共点 ,且这
,且这 个公共点均匀分布在直线
个公共点均匀分布在直线 上.(不要求过程)
上.(不要求过程)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(Ⅰ)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知幂函数 的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x-
的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x- 在(0,1)上为减函数.
在(0,1)上为减函数.
①求a的值;
②若 ,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足
,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足 ,
, ,求数列{an}的通项公式an和sn.
,求数列{an}的通项公式an和sn.
③设 ,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.
,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com