
| A. | 9-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | 6-$\sqrt{2}$ | D. | 6+$\sqrt{2}$ |
分析 涉及|PF|时,一般可以想到椭圆的定义,所以设该椭圆的右焦点为F′,则:|PF|+|PF′|=6,所以|PA|+|PF|=6+|PA|-|PF′|.这时候可以作出图形,根据图形即可看出||PA|-|PF′||≤|AF′|=$\sqrt{2}$,这样即可求得|PA|-|PF′|的最小值,从而求出|PA|+|PF|的最小值.
解答 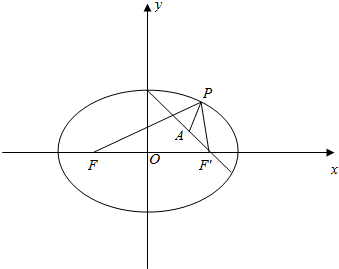 解:椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的a=3,b=$\sqrt{5}$,c=2,
解:椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的a=3,b=$\sqrt{5}$,c=2,
如图,设椭圆的右焦点为F'(2,0),
则|PF|+|PF′|=2a=6;
∴|PA|+|PF|=|PA|+6-|PF′|
=6+|PA|-|PF′|;
由图形知,当P在直线AF′上时,
||PA|-|PF′||=|AF′|=$\sqrt{2}$,
当P不在直线AF′上时,
根据三角形的两边之差小于第三边有,
||PA|-|PF′||<|AF′|=$\sqrt{2}$;
∴当P在F'A的延长线上时,|PA|-|PF′|取得最小值-$\sqrt{2}$,
∴|PA|+|PF|的最小值为6-$\sqrt{2}$.
故选:C.
点评 本题考查椭圆的标准方程,椭圆的焦点,以及椭圆的定义,以及三角形两边之差小于第三边,及数形结合求最值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=cos2πx | C. | y=cos[2(πx-$\frac{π}{4}$)]-$\frac{1}{2}$ | D. | y=tan$\frac{π}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:Rt△ABC中,∠ABC=90°,AB=BC.以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连OF.⊙C切⊙O于点D,交BC于G.
如图:Rt△ABC中,∠ABC=90°,AB=BC.以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连OF.⊙C切⊙O于点D,交BC于G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若x+y=0,则x,y互为相反数”的逆命题为真命题 | |
| B. | 命题“若xy=0,则x=0”的否命题为“若xy=0,则x≠0” | |
| C. | 命题“?x∈R,使得2x2-1<0”的否定是“?x∈R,均有2x2-1<0” | |
| D. | 命题“若cosx=cosy,则x=y”的逆否命题为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com