Question

3．太阳光线与地面的夹角为30°，一个球在地面的影子是椭圆，那么椭圆的离心率为（　　）

• A． $\frac{{\sqrt{3}}}{2}$
• B． $\frac{{\sqrt{3}}}{3}$
• C． $\frac{{2\sqrt{3}}}{3}$
• D． $\frac{1}{2}$

Answer 1

分析 首先要弄懂椭圆产生的原理，根据原理来解决三角形的边角关系，利用离心率公式求的结果．

解答 解：已知桌面上有一个球，半径为R，太阳光线与地面成30°角，
如图，l₁和l₂是两条与球相切的光线，分别切于点A和点C，分别与桌面交于点B和点D，则AC就是球的直径，BD的长就是椭圆的长轴长．过点A作AE∥BD，交l₂于点E，则BD=AE．在Rt△AEC中，因为∠AEC=30°，所以AE=$\frac{2R}{sin30°}$，即a=$\frac{R}{sin30°}$，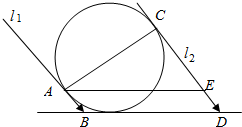

又因为b=R，所以c=$\sqrt{（\frac{R}{sin30°}）^{2}-{R}^{2}}$=$\frac{Rcos30°}{sin30°}$，
所以e=cos30°=$\frac{\sqrt{3}}{2}$．
故选：A．

点评 本题考查：椭圆产生的原理，a、b、c的关系式，求椭圆的离心率．