
【题目】已知函数![]() ,
,![]() ,
,
(1)求![]() 的解析式;
的解析式;
(2)关于![]() 的不等式
的不等式![]() 的解集为一切实数,求实数
的解集为一切实数,求实数![]() 的取值范围;
的取值范围;
(3)关于![]() 的不等式
的不等式![]() 的解集中的正整数解恰有
的解集中的正整数解恰有![]() 个,求实数
个,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)根据函数![]() 的解析式进行化简,即可求解;
的解析式进行化简,即可求解;
(2)由(1)化简![]() ,并分离参数,利用换元法,构造法求出函数的最值,即可求解;
,并分离参数,利用换元法,构造法求出函数的最值,即可求解;
(3)由(1)化简![]() ,结合条件将不等式化为
,结合条件将不等式化为![]() ,利用函数
,利用函数![]() 的性质,列出不等式,即可求解.
的性质,列出不等式,即可求解.
(1)由题意,函数![]() ,
,![]() ,则
,则![]() ,
,
所以函数![]() 的解析式
的解析式![]() ;
;
(2)由(1)和![]() ,可得
,可得![]() ,
,
即![]() 的解集为
的解集为![]() ,
,
设![]() ,则
,则![]() ,即
,即![]() ,
,
又由函数![]() 在
在![]() 为单调递增函数,
为单调递增函数,
所以当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,则
,则![]() ,
,
即实数![]() 的取值范围是
的取值范围是![]() .
.
(3)由(1)和![]() ,可得
,可得![]() ,
,
因为不等式![]() 的解集中正整数解恰好由3个,
的解集中正整数解恰好由3个,
所以当![]() 时,有
时,有![]() ,
,
若![]() ,则该不等式在
,则该不等式在![]() 上恒成立,与题设矛盾.
上恒成立,与题设矛盾.
故![]() ,所以
,所以![]() ,
,
设不等式![]() 的解集为
的解集为![]() ,
,
又由函数![]() 的性质和条件,
的性质和条件,
可得![]() ,所以
,所以![]() ,
,
解得![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某市坚持农业与旅游融合发展,着力做好旅游各要素,完善旅游业态,提升旅游接待能力.为了给游客提供更好的服务,旅游部门需要了解游客人数的变化规律,收集并整理了![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论正确的是( )
月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论正确的是( )
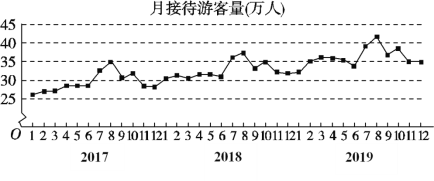
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
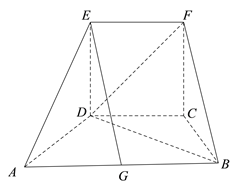
【题目】如图所示的几何体中,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.
(Ⅰ)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若存在区间
,若存在区间![]() 使得
使得![]() :
:
(Ⅰ)![]() 在
在![]() 上是单调函数;
上是单调函数;
(Ⅱ)![]() 在
在![]() 上的值域是
上的值域是![]() ,
,
则称区间![]() 为函数
为函数![]() 的“倍值区间”.
的“倍值区间”.
下列函数中存在“倍值区间”的有______________(填上所有你认为正确的序号)
①![]() ; ②
; ②![]() ;
;
③![]() ; ④
; ④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米,该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元平方米):
房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8 | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
(1)根据表格数据,完成下列茎叶图,并分别求出A,B两类户型住宅每平方米销售价格的中位数;
A户型 | B户型 | |
2. | ||
3. | ||
4. |
(2)该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号,每位购房者只有一次抽签机会,小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格,为了使其购房成功的概率更大,他应该选择哪一种户型抽签?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环线地铁按内、外环线同时运行,内、外环线的长均为30千米(忽略内、外环线长度差异).
(1)当9列列车同时在内环线上运行时,要使内环线乘客最长候车时间为10分钟,求内环线列车的最小平均速度;
(2)新调整的方案要求内环线列车平均速度为25千米/小时,外环线列车平均速度为30千米/小时.现内、外环线共有18列列车全部投入运行,要使内外环线乘客的最长候车时间之差不超过1分钟,向内、外环线应各投入几列列车运行?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com