
【题目】已知定义在区间[0,1]上的函数y=f(x)的图象如图所示.对满足0<x1<x2<1的任意x1,x2,给出下列结论:
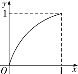
①f(x1)-f(x2)>x1-x2;
②f(x1)-f(x2)<x1-x2;
③x2f(x1)>x1f(x2);
④![]() .
.
其中正确结论的序号是________.
【答案】③④
【解析】
根据题意可作出函数![]() 的图象,根据直线的斜率的几何意义,利用数形结合的思想
的图象,根据直线的斜率的几何意义,利用数形结合的思想
研究函数的单调性与最值即可得到结论.
由于k=![]() 表示函数图象上两点(x1,f(x1)),(x2,f(x2))连线的斜率,当x1和x2都接近于零时,由图象可知k>1,
表示函数图象上两点(x1,f(x1)),(x2,f(x2))连线的斜率,当x1和x2都接近于零时,由图象可知k>1,
当x1和x2都接近于1时,k<1,
故①②均不正确;
当0<x1<x2<1时,根据斜率关系有![]() >
>![]() ,
,
即x2f(x1)>x1f(x2),所以③正确;
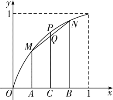
在区间(0,1)上任取两点A、B,其横坐标分别为x1,x2,过A、B分别作x轴的垂线,
与曲线交于点M、N,取AB中点C,过C作x轴的垂线,
与曲线交点为P,与线段MN交点为Q,
则![]() =CQ,f(
=CQ,f(![]() )=CP,
)=CP,
由图象易知CP>CQ,
故有![]() <f(
<f(![]() ),所以④正确.故答案为③④.
),所以④正确.故答案为③④.


科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:

(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试结束后,随机抽查了某校高三(1)班5名同学的数学与物理成绩如下表:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
(Ⅰ)分别求这5名同学数学与物理成绩的平均分与方差,并估计该班数学与物理成绩那科更稳定;
(Ⅱ)从以上5名同学中选2人参加一项活动,求选中的学生中至少有一个物理成绩高于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() ;
;
(2)已知![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)写出![]() 所有可能的零点个数及相应的
所有可能的零点个数及相应的![]() 的取值范围.(请直接写出结论)
的取值范围.(请直接写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球中没有红球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设![]() 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
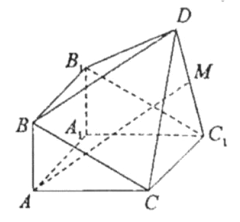
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com