
【题目】秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( ) 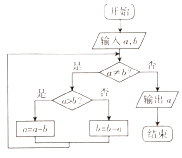
A.30
B.18
C.5
D.4
科目:高中数学 来源: 题型:
【题目】已知A(x1 , f(x1),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() . (Ⅰ)求函数f(x)的解析式;
. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)当x∈[0, ![]() ]时,求函数f(x)的单调递增区间;
]时,求函数f(x)的单调递增区间;
(Ⅲ)当x∈[0, ![]() ]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学从区间[﹣1,1]随机抽取2n个数x1 , x2 , …,xn , y1 , y2 , …,yn , 构成n个数对(x1 , y1),(x2 , y2),…(xn , yn),该同学用随机模拟的方法估计n个数对中两数的平方和小于1(即落在以原点为圆心,1为半径的圆内)的个数,则满足上述条件的数对约有个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在直角坐标系中,已知![]() ,若
,若![]() 。
。
(Ⅰ)求动点P的轨迹![]() 的方程;
的方程;
(Ⅱ)过点M的直线![]() 与(1)中轨迹
与(1)中轨迹![]() 相交于点A、B,求
相交于点A、B,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图: 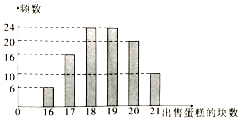
(1)若该蛋糕店某一天制作19块蛋糕,求当天的利润y(单位:元)关于当天需求量n的函数解析式;
(2)若要求出售“出售的蛋糕块数不小于n”的频率不小于0.4,求n的最大值.
(3)若该蛋糕店这100天每天都制作19块蛋糕,试计算这100天蛋糕店所获利润的平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com