练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设为平面直角坐标系内的点集，若对于任意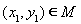，存在，使得，则称点集满足性质.给出下列三个点集：

    ①；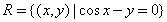

    ②；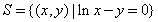

    ③.

    其中所有满足性质的点集的序号是______．

     

    【答案】

    ①③

    【解析】

    试题分析：设集合中的点，，构造向量，则，，由，则，故向量夹角为，分别画出图象，从图中观察，在②中，当点时，图象上不存在点B，使得.

    考点：1、向量的数量积运算及其性质；2、函数的图象和性质.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网设定义域为R的函数f(x)=
    |x+1|，x≤0
    (x-1)2，x＞0
    ．
    （1）在平面直角坐标系内作出该函数的图象；
    （2）试找出一组b和c的值，使得关于x的方程f2（x）+b•f（x）+c=0有7个不同的实根．请说明你的理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，AB为平面直角坐标系xOy中单位圆O的直径，点D在第二象限内的圆弧上运动，CD与圆O相切，切点为D，且CD=AB．设∠DAB=θ，问当θ取何值时，四边形ABCD的面积最大？并求出这个最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=(
    		x
    +
    		2
    )2(x＞0)    ，设正项数列an的首项a1=2，前n 项和Sn满足Sn=f（Sn-1）（n＞1，且n∈N*）．
    （1）求an的表达式；
    （2）在平面直角坐标系内，直线ln的斜率为an，且ln与曲线y=x2相切，ln又与y轴交于点Dn（0，bn），当n∈N*时，记dn=
    1
    4
    |
    Dn+1Dn
    |-1    ，若Cn=
    d
    2
    n+1
    +
    d
    2
    n
    2dn+1dn
    ，设Tn=C1+C2+C3+…+Cn，求
    lim
    n→∞
    n
    Tn
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网设定义域为R的函数f（x）=
    |x+1|，x≤0
    x2-2x+1，x＞0

    （Ⅰ）在平面直角坐标系内作出函数f（x）的图象，并指出f（x）的单调区间（不需证明）；
    （Ⅱ）若方程f（x）+2a=0有两个解，求出a的取值范围（只需简单说明，不需严格证明）．
    （Ⅲ）设定义为R的函数g（x）为奇函数，且当x＞0时，g（x）=f（x），求g（x）的解析式．

    查看答案和解析>>

    同步练习册答案