
【题目】求分别满足下列条件的直线l的方程:
(1)斜率是 ![]() ,且与两坐标轴围成的三角形的面积是6;
,且与两坐标轴围成的三角形的面积是6;
(2)经过两点A(1,0)、B(m,1);
(3)经过点(4,-3),且在两坐标轴上的截距的绝对值相等.
【答案】
(1)解:设直线l的方程为y= ![]() x+b.
x+b.
令y=0,得x=- ![]() b,
b,
∴ ![]() |b·(-
|b·(- ![]() b)|=6,b=±3.
b)|=6,b=±3.
∴直线l的方程为y= ![]() x±3.
x±3.
(2)解:当m≠1时,直线l的方程是
![]() ,即y=
,即y= ![]() (x-1)
(x-1)
当m=1时,直线l的方程是x=1.
(3)解:设l在x轴、y轴上的截距分别为a、b.
当a≠0,b≠0时,l的方程为 ![]() =1;
=1;
∵直线过P(4,-3),∴ ![]()
又∵|a|=|b|,
∴ 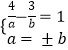 ,解得
,解得 ![]() ,或
,或 ![]() .
.
当a=b=0时,直线过原点且过(4,-3),
∴l的方程为y=- ![]() x.
x.
综上所述,直线l的方程为x+y=1或 ![]() =1或y=-
=1或y=- ![]() x.
x.
【解析】(1)先设出直线l的斜截式,再用含b的式子表示出直线l与两坐标轴的截距,再利用与两坐标轴围成的三角形的面积是6即可求得b的值,从而求得直线l的方程;(2)再利用两点式求直线的方程时需考虑是否直线与坐标轴平行,若平行则不能使用两点式;(3)先讨论截距不为0时的情况,设出直线l的截距式方程,再利用两坐标轴的截距绝对值相等即可求得直线l的方程;再讨论截距为0时的情况.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 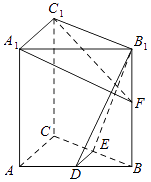
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定两个命题p:函数y=x2+8ax+1在[﹣1,1]上单调递增;q:方程 ![]() =1表示双曲线,如果命题“p∧q”为假命题,“p∨q”为真命题,求实数a的取值范围.
=1表示双曲线,如果命题“p∧q”为假命题,“p∨q”为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣4x+1.
( I)当x∈[0,3]时,画出函数y=f(x)的图象并写出值域;
(II)若函数y=f(x)在区间[a,a+1]上单调,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(1)已知点M(1,-3),N(1,2),P(5,y),且∠NMP=90°,则log8(7+y)=.
(2)若把本题中“∠NMP=90°”改为“log8(7+y)= ![]() ”,其他条件不变,则∠NMP=.
”,其他条件不变,则∠NMP=.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的倾斜角为135°,直线l1经过点A(3,2),B(a , -1),且l1与l垂直,直线l2:2x+by+1=0与直线l1平行,则a+b等于( )
A.-4
B.-2
C.0
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD= ![]() ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3 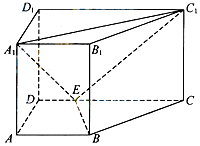
(1)证明:BE⊥平面BB1C1C;
(2)求三棱锥B1﹣EA1C1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com