已知m=
，n=
，满足
．
(1)将y表示为x的函数
，并求的最小正周期；
(2)已知a，b，c分别为
ABC的三个内角A，B，C对应的边长，
的最大值是
，且a=2，求b+c的取值范围．
科目：高中数学 来源： 题型：解答题
吉安一中新校区正在如火如荼地建设中，如图，某工地的平面图呈圆心角为120°的扇形AOB，工地的两个出入口设置在点A及点C处，工地中有两条笔直的小路AD、DC，长度分别为300米、500米，且DC平行于OB。求该扇形的半径OA的长（精确到1米）。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知
、
、
为正实数，
．
（1）当、、为
的三边长，且、、所对的角分别为
、
、
．若
，且
．求的长；
（2）若
．试证明长为、、的线段能构成三角形，而且边的对角为
．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知向量m＝
与n＝(3，sinA＋
cosA)共线，其中A是△ABC的内角．
(1)求角A的大小；
(2)若BC＝2，求△ABC面积S的最大值，并判断S取得最大值时△ABC的形状．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在△ABC中，角A，B，C的对边分别为a，b，c，若acos2
＋ccos2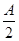
＝
b.
(1)求证：a，b，c成等差数列；
(2)若∠B＝60°，b＝4，求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，其最小正周期为
. （2）
. 
，及
，得到
． 
，
， 化简得到
，
利用
,进一步确定
的取值范围为
， 2分
，
，因为
， 10分
，
，
.
的单调增区间；
中，
分别是角
的对边，且
，求
，则
中，角
所对边分别为
，已知
.
的值；
，
求
的值.
的图像上两相邻最高点的坐标分别为
.
的值；
中，
分别是角
的对边，且
，求
的取值范围.