
已知函数 , 在
, 在 处取得极小值2.
处取得极小值2.
(1)求函数 的解析式;
的解析式;
(2)求函数 的极值;
的极值;
(3)设函数 , 若对于任意
, 若对于任意 ,总存在
,总存在 , 使得
, 使得 , 求实数
, 求实数  的取值范围.
的取值范围.
(1)函数 的解析式为
的解析式为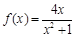 ;(2)
;(2)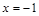 时,函数
时,函数 有极小值-2;当
有极小值-2;当 时,函数
时,函数 有极大值2 ;(3)a的取值范围是(-∞,-1]∪[ 3,+∞).
有极大值2 ;(3)a的取值范围是(-∞,-1]∪[ 3,+∞).
解析试题分析:(1)根据函数在极值处导函数为0,极小值为2联立方程组即可求得m,n;(2)由(1)求得函数解析式,对函数求导且让导函数为0,即可求得极大值和极小值;(3)依题意只需
科目:高中数学
来源:
题型:解答题
甲方是一农场,乙方是一工厂.由于乙方生产需占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系x=2 000
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
如图,现要在边长为
科目:高中数学
来源:
题型:解答题
已知函数f(x)=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 即可,当
即可,当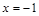 时,函数
时,函数 有最小值-2 ,即对任意
有最小值-2 ,即对任意 总存在
总存在 ,使得
,使得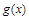 的最小值不大于-2 ;而
的最小值不大于-2 ;而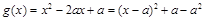 ,分
,分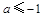 、
、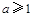 、
、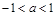 三种情况讨论即可.
三种情况讨论即可.
试题解析:(1)∵函数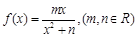 在
在 处取得极小值2,∴
处取得极小值2,∴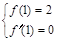 1分
1分
又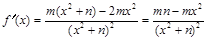 ∴
∴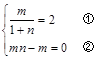
由②式得m=0或n=1,但m=0显然不合题意 ∴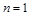 ,代入①式得m=4
,代入①式得m=4
∴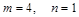 2分
2分
经检验,当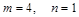 时,函数
时,函数 在
在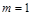 处取得极小值2
处取得极小值2
∴函数 的解析式为
的解析式为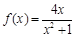 4分
4分
(2)∵函数 的定义域为
的定义域为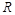 且由(1)有
且由(1)有 
令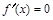 ,解得:
,解得: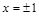
∴当x变化时,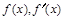 的变化情况如下表:
的变化情况如下表:x (-∞,-1) -1 (-1,1) 1 (1,+∞) 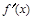
— 0 + 0 — 
减 极小值-2


1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
 .若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
.若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
(1)将乙方的年利润w(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙方生产影响的经济损失金额y=0.002t2(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格S是多少? ,其中
,其中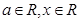 .
.
(1)当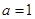 时,求函数
时,求函数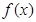 在
在 处的切线方程;
处的切线方程;
(2)若函数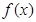 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求 的取值范围;
的取值范围;
(3)已知 ,如果存在
,如果存在 ,使得函数
,使得函数
 在
在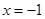 处取得最小值,试求
处取得最小值,试求 的最大值.
的最大值. 的正方形
的正方形 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为
内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为 (
( 不小于
不小于 )的扇形花坛,以正方形的中心为圆心建一个半径为
)的扇形花坛,以正方形的中心为圆心建一个半径为 的圆形草地.为了保证道路畅通,岛口宽不小于
的圆形草地.为了保证道路畅通,岛口宽不小于 ,绕岛行驶的路宽均不小于
,绕岛行驶的路宽均不小于 .
.
(1)求 的取值范围;(运算中
的取值范围;(运算中 取
取 )
)
(2)若中间草地的造价为 元
元 ,四个花坛的造价为
,四个花坛的造价为 元
元 ,其余区域的造价为
,其余区域的造价为 元
元 ,当
,当 取何值时,可使“环岛”的整体造价最低?
取何值时,可使“环岛”的整体造价最低? 在x=0,x=
在x=0,x= 处存在极值。
处存在极值。
(Ⅰ)求实数a,b的值;
(Ⅱ)函数y=f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围;
(Ⅲ)当c=e时,讨论关于x的方程f(x)=kx(k∈R)的实根个数。
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号