
分析 由题设中的定义,可对x分区间讨论,设m表示整数,综合此四类即可得到函数的值域
解答 解:设m表示整数.
①当x=2m时,[$\frac{x+1}{2}$]=[m+0.5]=m,[$\frac{x}{2}$]=[m]=m.
∴此时恒有y=0.
②当x=2m+1时,[$\frac{x+1}{2}$]=[m+1]=m+1,[$\frac{x}{2}$]=[m+0.5]=m.
∴此时恒有y=1.
③当2m<x<2m+1时,
2m+1<x+1<2m+2
∴m<$\frac{x}{2}$<m+0.5
m+0.5<$\frac{x+1}{2}$<m+1
∴[$\frac{x}{2}$]=m,[$\frac{x+1}{2}$]=m
∴此时恒有y=0
④当2m+1<x<2m+2时,
2m+2<x+1<2m+3
∴m+0.5<$\frac{x}{2}$<m+1
m+1<$\frac{x+1}{2}$<m+1.5
∴此时[$\frac{x}{2}$]=m,[$\frac{x+1}{2}$]=m+1
∴此时恒有y=1.
综上可知,y∈{0,1}.
故答案为{0,1}.
点评 此题是新定义一个函数,根据所给的规则求函数的值域,求解的关键是理解所给的定义,一般从函数的解析式入手,要找出准确的切入点,理解[x]表示数x的整数部分,考察了分析理解,判断推理的能力及分类讨论的思想


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
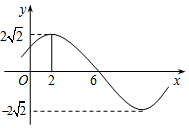
| A. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{3π}{4}$ | B. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{π}{4}$ | C. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{π}{2}$ | D. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 梯形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com