
【题目】设![]() 是不小于3的正整数,集合
是不小于3的正整数,集合![]() ,对于集合
,对于集合![]() 中任意两个元素
中任意两个元素![]() ,
,![]() .
.
定义1:![]() .
.
定义2:若![]() ,则称
,则称![]() ,
,![]() 互为相反元素,记作
互为相反元素,记作![]() ,或
,或![]() .
.
(Ⅰ)若![]() ,
,![]() ,
,![]() ,试写出
,试写出![]() ,
,![]() ,以及
,以及![]() 的值;
的值;
(Ⅱ)若![]() ,证明:
,证明:![]() ;
;
(Ⅲ)设![]() 是小于
是小于![]() 的正奇数,至少含有两个元素的集合
的正奇数,至少含有两个元素的集合![]() ,且对于集合
,且对于集合![]() 中任意两个不相同的元素
中任意两个不相同的元素![]() ,
,![]() ,都有
,都有![]() ,试求集合
,试求集合![]() 中元素个数的所有可能值.
中元素个数的所有可能值.
【答案】(Ⅰ)2;(Ⅱ)详见解析;(Ⅲ)2.
【解析】
(Ⅰ)根据定义求![]() ,
,![]() ,以及
,以及![]() 的值;(Ⅱ)设
的值;(Ⅱ)设![]() ,
,![]() ,根据定义求
,根据定义求![]() ,再根据定义化简
,再根据定义化简![]() ,即得结果,(Ⅲ)先假设集合
,即得结果,(Ⅲ)先假设集合![]() 有三个不相同的元素
有三个不相同的元素![]() ,
,![]() ,
,![]() ,再根据
,再根据![]() 得
得![]() 恰有
恰有![]() 个1,与
个1,与![]() 个0,同理可得
个0,同理可得![]() 恰有
恰有![]() 个1,与
个1,与![]() 个0,调整次序对应相减可得
个0,调整次序对应相减可得![]() ,最后根据
,最后根据![]()
![]()
![]() 为奇数,得到矛盾,否定假设,即得结果.
为奇数,得到矛盾,否定假设,即得结果.
(Ⅰ)![]() ,
,![]() ,
,![]()
(Ⅱ)设![]() ,
,![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,
,![]()
所以![]() ,
,
当且仅当![]() ,
,![]() ,即
,即![]() ,
,![]() 时上式“=”成立
时上式“=”成立
由题意可知![]()
即![]()
所以![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
(Ⅲ)解法1:假设![]() ,
,![]() ,
,![]() 为集合
为集合![]() 中的三个不相同的元素.
中的三个不相同的元素.
则![]()
即![]()
又由题意可知![]() 或1,
或1,![]()
![]() 恰有
恰有![]() 个1,与
个1,与![]() 个0
个0
设其中![]() 个等于1的项依次为
个等于1的项依次为![]()
![]() 个等于0的项依次为
个等于0的项依次为![]()
由题意可知![]()
所以![]() ,同理
,同理![]()
所以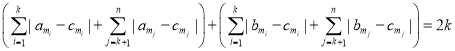
即![]()
因为![]()
由(2)可知![]()
因为![]()
所以![]() ,
,
设![]() ,由题意可知
,由题意可知![]()
所以![]() ,得
,得![]() 与
与![]() 为奇数矛盾
为奇数矛盾
所以假设不成立,即集合![]() 中至多有两个元素
中至多有两个元素
当![]() 时符合题意
时符合题意
所以集合![]() 中元素的个数只可能是2
中元素的个数只可能是2
解法2:假设![]() ,
,![]() ,
,![]() 为集合
为集合![]() 中的三个不相同的元素.
中的三个不相同的元素.
则![]()
即![]()
又由题意可知![]() 或1,
或1,![]()
![]() 恰有
恰有![]() 个1,与
个1,与![]() 个0
个0
设其中![]() 个等于1的项依次为
个等于1的项依次为![]()
![]() 个等于0的项依次为
个等于0的项依次为![]()
由题意可知![]()
所以![]() ①
①
同理![]() ②
②
①—②得![]()
又因为![]()
![]()
![]() 为奇数
为奇数
与![]() 矛盾
矛盾
所以假设不成立,即集合![]() 中至多有两个元素
中至多有两个元素
当![]() 时符合题意
时符合题意
所以集合![]() 中元素的个数只可能是2
中元素的个数只可能是2


科目:高中数学 来源: 题型:
【题目】将函数 ![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的 ![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则下列说法正确的是( )
个单位长度,得到函数y=g(x)的图象,则下列说法正确的是( )
A.函数g(x)的一条对称轴是 ![]()
B.函数g(x)的一个对称中心是 ![]()
C.函数g(x)的一条对称轴是 ![]()
D.函数g(x)的一个对称中心是 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列{an}的各项都是正数,其前n项和为Sn , 且满足:a1=a,rSn=anan+1﹣1,其中a≠1,常数r∈N;
(1)求证:an+2﹣an是一个定值;
(2)若数列{an}是一个周期数列(存在正整数T,使得对任意n∈N* , 都有an+T=an成立,则称{an}为周期数列,T为它的一个周期,求该数列的最小周期;
(3)若数列{an}是各项均为有理数的等差数列,cn=23n﹣1(n∈N*),问:数列{cn}中的所有项是否都是数列{an}中的项?若是,请说明理由,若不是,请举出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C1: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.
,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长. 
(Ⅰ)求C1 , C2的方程;
(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.
(i)证明:MD⊥ME;
(ii)记△MAB,△MDE的面积分别是S1 , S2 . 问:是否存在直线l,使得 ![]() =
= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解本校学生的身体素质情况,决定在全校的1000名男生和800名女生中按分层抽样的方法抽取45名学生对他们课余参加体育锻炼时间进行问卷调查,将学生课余参加体育锻炼时间的情况分三类:A类(课余参加体育锻炼且平均每周参加体育锻炼的时间超过3小时),B类(课余参加体育锻炼但平均每周参加体育锻炼的时间不超过3小时),C类(课余不参加体育锻炼),调查结果如表:
A类 | B类 | C类 | |
男生 | 18 | x | 3 |
女生 | 10 | 8 | y |
(1)求出表中x、y的值;
(2)根据表格统计数据,完成下面的列联表,并判断是否有90%的把握认为课余参加体育锻炼且平均每周参加体育锻炼的时间超过3小时与性别有关;
男生 | 女生 | 总计 | |
A类 | |||
B类和C类 | |||
总计 |
(3)在抽取的样本中,从课余不参加体育锻炼学生中随机选取三人进一步了解情况,求选取三人中男女都有且男生比女生多的概率. 附:K2= ![]()
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处发现北偏东
处发现北偏东![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处有一艘走私船.在
处有一艘走私船.在![]() 处北偏西
处北偏西![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处的我方缉私船奉命以
处的我方缉私船奉命以![]() 海里
海里![]() 小时的速度追截走私船,此时走私船正以
小时的速度追截走私船,此时走私船正以![]() 海里
海里![]() 小时的速度从
小时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623——1662)是在1654年发现这一规律的,比杨辉要迟![]() 年,比贾宪迟
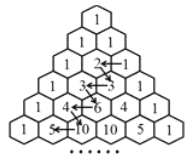
年,比贾宪迟![]() 年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了,这又是我国数学史上的一个伟大成就。如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:
年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了,这又是我国数学史上的一个伟大成就。如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:![]() ,则此数列前
,则此数列前![]() 项和为________.
项和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
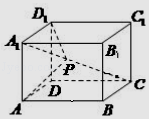
【题目】如图,在长方体ABCD﹣A1B1C1D1中, ![]() ,点P为线段A1C上的动点(包含线段端点),则下列结论正确的 . ①当
,点P为线段A1C上的动点(包含线段端点),则下列结论正确的 . ①当 ![]() 时,D1P∥平面BDC1;
时,D1P∥平面BDC1;
②当 ![]() 时,A1C⊥平面D1AP;
时,A1C⊥平面D1AP;
③当∠APD1的最大值为90°;
④AP+PD1的最小值为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com