
| 优秀 | 非优秀 | 总计 | |
| A班 | 14 | 6 | 20 |
| B班 | 7 | 13 | 20 |
| C班 | 21 | 19 | 40 |
 (其中n=n11+n12+n21+n22);
(其中n=n11+n12+n21+n22);| P(x2≥k) | 0.050 | 0.010 |
| K | 3.841 | 6.635 |


科目:高中数学 来源: 题型:
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为mo,平均值为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为mo,平均值为. |
| x |
A、me=mo=
| ||
B、me=mo<
| ||
C、me<mo<
| ||
D、mo<me<
|
查看答案和解析>>
科目:高中数学 来源: 题型:

| 优秀 | 非优秀 | 总计 | |
| A班 | 20 | ||
| B班 | 20 | ||
| 总计 | 40 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
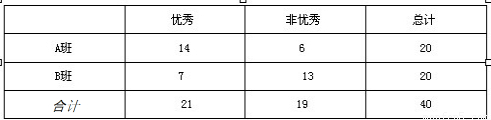
(2012•潍坊二模)为了普及环保知识,增强环保意识,某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试.统计得到成绩与专业的列联表:
(1)卡方统计量x2=
(2)独立性检验的临界值表:
|
查看答案和解析>>
科目:高中数学 来源: 题型:

| 优秀 | 非优秀 | 总计 | |
| A班 | 20 | ||
| B班 | 20 | ||
| 合计 | 40 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2011年江西省招生考试文科数学 题型:选择题
为了普及环保知识,增强环保意识,某大学随即抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为 ,众数为
,众数为 ,平均值为
,平均值为 ,则( )
,则( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com