
【题目】已知函数f(x)+2= ![]() ,当x∈(0,1]时,f(x)=x2 , 若在区间(﹣1,1]内,g(x)=f(x)﹣t(x+2)有两个不同的零点,则实数t的取值范围是( )
,当x∈(0,1]时,f(x)=x2 , 若在区间(﹣1,1]内,g(x)=f(x)﹣t(x+2)有两个不同的零点,则实数t的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
科目:高中数学 来源: 题型:
【题目】近期“共享单车”在全国多个城市持续升温,某移动互联网机构通过对使用者的调查得出,现在市场上常见的八个品牌的“共享单车”的满意度指数如茎叶图所示:
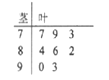
(Ⅰ)求出这组数据的平均数和中位数;
(Ⅱ)某用户从满意度指数超过80的品牌中随机选择两个品牌使用,求所选两个品牌的满意度指数均超过85的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(4)与f(8)的值;
(2)解不等式f(x)﹣f(x﹣2)>3.
查看答案和解析>>
科目:高中数学 来源: 题型:
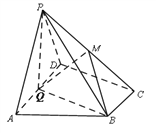
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面ABCD,Q为AD的中点,M是棱
底面ABCD,Q为AD的中点,M是棱![]() 上的点,
上的点, ![]()
(Ⅰ)若![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ;
;
(Ⅱ)若二面角![]() 的大小为
的大小为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的左右顶点分别为A(﹣2,0),B(2,0),椭圆上除A、B外的任一点C满足kACkBC=﹣ ![]() .
. 
(1)求椭圆C的标准方程;
(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N,在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明现由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com