
����Ŀ��ij��ѧһλ���������ζԱ���50��ѧ��ѧϰ�����ԺͶԴ��༶������̬�Ƚ��е��飬�õ���ͳ�����������ʾ��
�����μӰ༶���� | �������μӰ༶���� | �ϼ� | |
ѧϰ�����Ը� | 18 | 7 | 25 |
ѧϰ�����Բ��� | 6 | 19 | 25 |
�ϼ� | 24 | 26 | 50 |
��1������������������һ��ѧ������ô�鵽�������μӰ༶������ѧϰ�����Բ��ߵ�ѧ���ĸ����Ƕ��٣�
��2�����������μӰ༶������ѧϰ�����Ըߵ�7��ѧ�����������������ִ��г�ȡ2��ѧ���μ�ij������2��ѧ������1�������ĸ����Ƕ��٣�
��3��ѧ����ѧϰ��������Դ��༶������̬���Ƿ��й�ϵ����˵�����ɣ�
����

![]()
���𰸡���1��![]() ����2��
����2��![]() ����3����
����3����![]() �İ�����Ϊ��ѧ����ѧϰ��������Դ��༶������̬�ȡ��й�ϵ
�İ�����Ϊ��ѧ����ѧϰ��������Դ��༶������̬�ȡ��й�ϵ
�����������������������Ҫ���������������塢���ʵȻ���֪ʶ������ѧ���ķ��������������������ת��������������������һ�ʣ�����֪����֪���������μӰ༶������ѧϰ�����Բ��ߵ�ѧ����19�ˣ�������Ϊ50�ˣ�����![]() ���ڶ��ʣ���7��ѧ������ĸ��ʾ�������ô�Сд��ĸ������Ů�����ֿ����������ȡ2��ѧ�����������ȫ����ʾ������������ѡ�������������������������ʣ������ʣ�������֪�Ĺ�ʽ�����
���ڶ��ʣ���7��ѧ������ĸ��ʾ�������ô�Сд��ĸ������Ů�����ֿ����������ȡ2��ѧ�����������ȫ����ʾ������������ѡ�������������������������ʣ������ʣ�������֪�Ĺ�ʽ�����![]() ���ٸ��ݱ����ж��Ƿ��а�����Ϊ��ѧ����ѧϰ��������Դ��༶������̬�����й�ϵ��
���ٸ��ݱ����ж��Ƿ��а�����Ϊ��ѧ����ѧϰ��������Դ��༶������̬�����й�ϵ��
���������������![]() ����������7��ѧ��Ϊa��b��c��d��e��A��B����дΪ������������г�ȡ����ѧ������������ǣ�ab��ac��ad��ae��aA��aB��bc��bd��be��bA��Bb��cd��ce��cA��cB��de��dA��dB��eA��eB��AB��21����������к�һ����������10���������
����������7��ѧ��Ϊa��b��c��d��e��A��B����дΪ������������г�ȡ����ѧ������������ǣ�ab��ac��ad��ae��aA��aB��bc��bd��be��bA��Bb��cd��ce��cA��cB��de��dA��dB��eA��eB��AB��21����������к�һ����������10���������![]()
����������![]()
��������99��9%������Ϊ��ѧ����ѧϰ��������Դ��༶������̬�����й�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��ֱ��
��ֱ��![]() ���ڵ�ƽ��
���ڵ�ƽ��![]() ��
��![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() �ǻ�
�ǻ�![]() �ϵ�һ�����㣨����˵�
�ϵ�һ�����㣨����˵�![]() �غϣ���
�غϣ���![]() Ϊ
Ϊ![]() ��һ�㣬��
��һ�㣬��![]() ���߶�
���߶�![]() �ϵ�һ�����㣨����˵�
�ϵ�һ�����㣨����˵�![]() �غϣ�.
�غϣ�.

��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����![]() �ǻ�
�ǻ�![]() ���е㣬
���е㣬![]() ����ǣ�������
����ǣ�������![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ�����пƽ̴�Ϊ���о���һѧ������������ѧ��ѧϰ�Ƿ����Ա��йأ��Ӹ�һ�꼶��ȡ60,��ͬѧ����ͬѧ30����Ůͬѧ30������������ͬѧ���������ѧ���һ�⣬��ÿλͬѧ����ѡ��һ������н��.ѡ��������±�������λ���ˣ�

��1���ڷ�����ĸ��ʲ�����1%�������£��ܷ��жϸ�һѧ������������ѧ��ѧϰ���Ա��йأ�
��2��������β��Ժ��֣���ÿ�ν��һ�����������õ�ʱ��5��8���ӣ���ÿ�ν��һ�����������õ�ʱ��Ϊ6��8���ӣ��ּס��ҽ�ͬһ�������⣬��ױ����Ƚ����ĸ��ʣ�
��3���ִ�ѡ�����������8��Ů��������ѡȡ���ˣ�����Ŀ�Ľ���������ȫ���о����Ǽס�����Ů�����鵽������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��R�ϵ�ż����������
��R�ϵ�ż����������![]() ����
����![]() ��������
��������![]() ����
����![]() ����
����![]() ʱ������
ʱ������![]() ��������������⣺
��������������⣺
��![]() ��
��
������![]() ͼ���һ���Գ���Ϊ
ͼ���һ���Գ���Ϊ![]() ��
��
������![]() ��[��9����6]����������������
��[��9����6]����������������![]() ��[��9��9]����4������
��[��9��9]����4������
������ȷ�����������___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() �IJ���ͼ����ͼ��ʾ��
�IJ���ͼ����ͼ��ʾ��

��1�������Ľ���ʽ��
��2����![]() ���ҷ���
���ҷ���![]() ��������ͬ��ʵ��������ʵ��
��������ͬ��ʵ��������ʵ��![]() ��ȡֵ��Χ�����������ĺ�
��ȡֵ��Χ�����������ĺ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��1000��ѧ���������ȡ��100��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ.
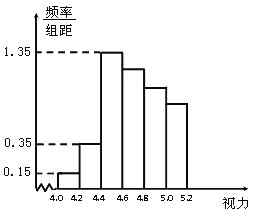

��1����ֱ��ͼ�к������Ƶ���ɵȲ����У��Թ���ȫ�꼶������5.0���µ�������
��2��ѧϰС���Ա���֣�ѧϰ�ɼ�ͻ����ѧ�������ӵıȽ϶࣬Ϊ���о�ѧ����������ѧϰ�ɼ��Ƿ��й�ϵ�����꼶������1��50����951��1000����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��3���ڣ�2���е����100��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��9�ˣ���һ�������������õĻ���ϰ�ߣ���������9������ȡ3�ˣ���������1��50��ѧ������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
����

![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������14�֣�
��֪����![]() ��ͼ����
��ͼ����![]() ���������ϣ����壺
���������ϣ����壺
![]()
![]() ��
��
![]()
![]() ��
��
���У�![]() ��ʾ����
��ʾ����![]() ��
��![]() �ϵ���Сֵ��
�ϵ���Сֵ��![]() ��ʾ����
��ʾ����![]() ��
��![]() �ϵ����ֵ����������С������
�ϵ����ֵ����������С������![]() ��ʹ��
��ʹ��![]() �������
�������![]() ��������ƺ���
��������ƺ���![]() Ϊ
Ϊ![]() �ϵ���
�ϵ���![]() ��������������
��������������
��������![]() ��
��![]() �����
�����![]() ��
��![]() �ı���ʽ��
�ı���ʽ��
��������֪����![]() ��
��![]() �����ж�
�����ж�![]() �Ƿ�Ϊ
�Ƿ�Ϊ![]() �ϵ���
�ϵ���![]() ������������������ǣ������Ӧ��
������������������ǣ������Ӧ��![]() ��������ǣ���˵�����ɣ�
��������ǣ���˵�����ɣ�
��������֪![]() ������
������![]() ��
��![]() �ϵ�2��������������
�ϵ�2��������������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ����Բ![]() ���ҽ���
���ҽ���![]() �Ķ�ֱ��
�Ķ�ֱ��![]() �ཻ��
�ཻ��![]() �㣬����Բ
�㣬����Բ![]() �ֱ���
�ֱ���![]() ��
��![]() ��ͬ���㣬ֱ��
��ͬ���㣬ֱ��![]() ��б��
���![]() ����
����![]() , ��֪
, ��֪![]() ��
��![]() ���غ�ʱ,
���غ�ʱ, ![]() .
.
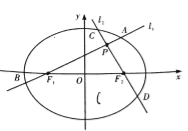
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2���Ƿ���ڶ���![]() ʹ��
ʹ��![]() Ϊ��ֵ�������ڣ����
Ϊ��ֵ�������ڣ����![]() �����겢����˶�ֵ���������ڣ�
�����겢����˶�ֵ���������ڣ�
˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ����
����![]() ��
��![]() Ϊֱ�ǣ�
Ϊֱ�ǣ�![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е�.
���е�.

��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��ƽ��
��ƽ��![]() ���ɽǵĴ�С��
���ɽǵĴ�С��
��3��������![]() �����.
�����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com