
【题目】设函数![]() (其中
(其中![]() ,m,n为常数)
,m,n为常数)
(1)当![]() 时,对
时,对![]() 有
有![]() 恒成立,求实数n的取值范围;
恒成立,求实数n的取值范围;
(2)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() 的零点为
的零点为![]() ,求所有满足
,求所有满足![]() 的整数k的和.
的整数k的和.
科目:高中数学 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下侧的图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
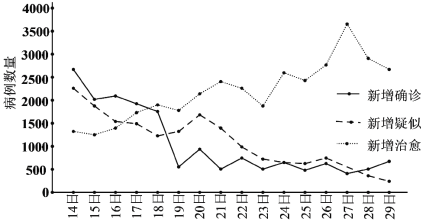
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数大于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于![]()
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新型冠状病毒肺炎(COVID-19)在我国爆发,全国人民团结一心、积极抗疫,为全世界疫情防控争取了宝贵的时间,积累了丰富的经验.某研究小组为了研究某城市肺炎感染人数的增长情况,在官方网站.上搜集了7组数据,并依据数据制成如下散点图:
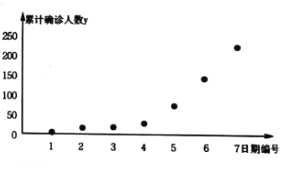
图中![]() 表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型
表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型![]() 来拟合,为求出
来拟合,为求出![]() 关于
关于![]() 的回归方程,可令
的回归方程,可令![]() ,则
,则![]() 与
与![]() 线性相关.初步整理后,得到如下数据:
线性相关.初步整理后,得到如下数据:![]() ,
,![]() .
.
(1)根据所给数据,求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
(2)求![]() 关于
关于![]() 的回归方程;若防控不当,请问
的回归方程;若防控不当,请问![]() 为何值时,累计确诊人数的预报值将超过1000人?(参考数据:
为何值时,累计确诊人数的预报值将超过1000人?(参考数据:![]() ,结果保留整数)
,结果保留整数)
附:对于一组数据![]() ,其线性回归方程
,其线性回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为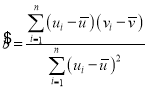 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为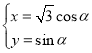 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上位于第一,二象限的两个动点,且
上位于第一,二象限的两个动点,且![]() ,射线
,射线![]() 交曲线
交曲线![]() 分别于
分别于![]() ,求
,求![]() 面积的最小值,并求此时四边形
面积的最小值,并求此时四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C关于x轴、y轴都对称,并且经过两点![]() ,
,
(1)求椭圆C的离心率和焦点坐标;
(2)D是椭圆C上到点A最远的点,椭圆C在点B处的切线l与y轴交于点E,求△BDE外接圆的圆心坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.
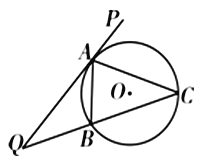
(Ⅰ)求证:QC2﹣QA2=BC![]() QC;
QC;
(Ⅱ)求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷集合A,B,且![]() ,
,![]() ,记
,记![]() ,定义:满足
,定义:满足![]() 时,则称集合A,B互为“完美加法补集”.
时,则称集合A,B互为“完美加法补集”.
(Ⅰ)已知集合![]() ,
,![]() .判断2019和2020是否属于集合
.判断2019和2020是否属于集合![]() ,并说明理由;
,并说明理由;
(Ⅱ)设集合![]() ,
,![]() .
.
(ⅰ)求证:集合A,B互为“完美加法补集”;
(ⅱ)记![]() 和
和![]() 分别表示集合A,B中不大于n(
分别表示集合A,B中不大于n(![]() )的元素个数,写出满足
)的元素个数,写出满足![]() 的元素n的集合.(只需写出结果,不需要证明)
的元素n的集合.(只需写出结果,不需要证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有教职工120人,对他们进行年龄结构和受教育程度的调查,其结果如下表:
本科 | 研究生 | 合计 | |
35岁以下 | 40 | 30 | 70 |
35-50岁 | 27 | 13 | 40 |
50岁以上 | 8 | 2 | 10 |
现从该校教职工中任取1人,则下列结论正确的是( )
A.该教职工具有本科学历的概率低于60%
B.该教职工具有研究生学历的概率超过50%
C.该教职工的年龄在50岁以上的概率超过10%
D.该教职工的年龄在35岁及以上且具有研究生学历的概率超过10%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线G上的点到点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小2.
的距离小2.
(1)求曲线G的方程.
(2)是否存在过F的直线l,使得l与曲线G相交于A,B两点,点A关于x轴的对称点为A',且△A'BF的面积等于4?若存在,求出此时直线l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com