
【题目】如图,四棱锥![]() 中,
中,![]() ,底面
,底面![]() 是梯形,AB∥CD,
是梯形,AB∥CD,![]() ,AB=PD=4,CD=2,
,AB=PD=4,CD=2,![]() ,M为CD的中点,N为PB上一点,且
,M为CD的中点,N为PB上一点,且![]() .
.
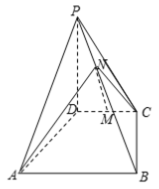
(1)若![]() MN∥平面PAD;
MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为![]() ,求异面直线AD与直线CN所成角的余弦值.
,求异面直线AD与直线CN所成角的余弦值.
【答案】(1)见解析(2) ![]()
【解析】(1)当![]() 时,
时,![]() 在PA上取点E,使得
在PA上取点E,使得![]() ,连接EN,DE,
,连接EN,DE,
![]()
![]() ,
,
![]() EN∥AB,且
EN∥AB,且![]() ,
,
![]() M为CD的中点,CD=2,
M为CD的中点,CD=2,
![]() ,
,
又AB∥CD,![]() EN∥DM,EN=DM,
EN∥DM,EN=DM,
![]() 四边形DMNE是平行四边形,
四边形DMNE是平行四边形,
![]() MN∥DE,
MN∥DE,
又![]()
![]() 平面PAD,MN
平面PAD,MN![]() 平面PAD,
平面PAD,
![]() MN∥平面PAD.
MN∥平面PAD.
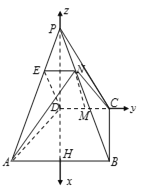
(2)如图所示,过点D作DH![]() AB于H,则DH
AB于H,则DH![]() CD.以D为坐标原点建立空间直角坐标系Dxyz.
CD.以D为坐标原点建立空间直角坐标系Dxyz.
则D(0,0,0),M(0,1,0),C(0,2,0),B(2,2,0),A(2,2,0),P(0,0,4),
∴![]() ,
,![]()
![]() .
.
该平面BC的法向量为![]() ,则由
,则由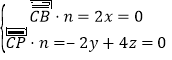 ,得
,得![]() ,令z=1,得
,令z=1,得![]() .
.
该直线AN与平面PBC所成的角为![]() ,则
,则
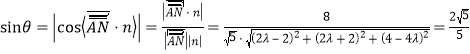 ,解得
,解得![]()
∴![]() ,
,
设直线AD与直线CN所成的角为![]() ,
,
则![]() .
.
所以直线AD与直线CN所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】有120粒试验种子需要播种,现有两种方案:方案一:将120粒种子分种在40个坑内,每坑3粒;方案二:120粒种子分种在60个坑内,每坑2粒 如果每粒种子发芽的概率为0.5,并且,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种(每个坑至多补种一次,且第二次补种的种子颗粒同第一次).假定每个坑第一次播种需要2元,补种1个坑需1元;每个成活的坑可收货100粒试验种子,每粒试验种子收益1元.
(1)用![]() 表示播种费用,分别求出两种方案的
表示播种费用,分别求出两种方案的![]() 的数学期望;
的数学期望;
(2)用![]() 表示收益,分别求出两种方案的收益
表示收益,分别求出两种方案的收益![]() 的数学期望;
的数学期望;
(3)如果在某块试验田对该种子进行试验,你认为应该选择哪种方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车的春天来了!2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.某人计划于2018年5月购买一辆某品牌新能源汽车,他从当地该品牌销售网站了解到近五个月实际销量如下表:
月份 | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
月份编号t | 1 | 2 | 3 | 4 | 5 |
销量(万辆) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析,可用线性回归模型拟合当地该品牌新能源汽车实际销量![]() (万辆)与月份编号
(万辆)与月份编号![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测2018年5月份当地该品牌新能源汽车的销量;
,并预测2018年5月份当地该品牌新能源汽车的销量;
(2)2018年6月12日,中央财政和地方财政将根据新能源汽车的最大续航里程(新能源汽车的最大续航里程是指理论上新能源汽车所装的燃料或电池所能够提供给车跑的最远里程)对购车补贴进行新一轮调整.已知某地拟购买新能源汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
补贴金额预期值区间(万元) |
|
|
|
|
|
|
20 | 60 | 60 | 30 | 20 | 10 |
将频率视为概率,现用随机抽样方法从该地区拟购买新能源汽车的所有消费者中随机抽取3人,记被抽取3人中对补贴金额的心理预期值不低于3万元的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式及数据:①回归方程![]() ,其中
,其中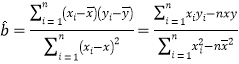 ,
,![]() ,②
,②![]() ,.
,.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代“五行”学认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有
A.5种B.10种
C.20种D.120种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月20日,辽宁省人民政府公布了“![]() ”新高考方案,方案中“2”指的是在思想政治、地理、化学、生物4门中选择2门.“2”中记入高考总分的单科成绩是由原始分转化得到的等级分,学科高考原始分在全省的排名越靠前,等级分越高.小明同学是2018级的学生.已确定了必选地理且不选政治,为确定另选一科,小明收集并整理了生物与化学近10大联考的成绩百分比排名数据x(如
”新高考方案,方案中“2”指的是在思想政治、地理、化学、生物4门中选择2门.“2”中记入高考总分的单科成绩是由原始分转化得到的等级分,学科高考原始分在全省的排名越靠前,等级分越高.小明同学是2018级的学生.已确定了必选地理且不选政治,为确定另选一科,小明收集并整理了生物与化学近10大联考的成绩百分比排名数据x(如![]() 的含义是指在该次考试中,成绩高于小明的考生占参加该次考试的考生数的
的含义是指在该次考试中,成绩高于小明的考生占参加该次考试的考生数的![]() )绘制茎叶图如下.
)绘制茎叶图如下.

则由图中数据生物学科联考百分比排名的![]() 分位数为________.从平均数的角度来看你认为小明更应该选择________.(填生物或化学)
分位数为________.从平均数的角度来看你认为小明更应该选择________.(填生物或化学)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在极坐标系中,点![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点,以极点为原点,极轴为
的中点,以极点为原点,极轴为![]() 轴的正半轴,并在两坐标系中取相同的长度单位,建立平面直角坐标系,曲线
轴的正半轴,并在两坐标系中取相同的长度单位,建立平面直角坐标系,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 过点
过点![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数 .
.
(1)求实数![]() 的值,并画出函数
的值,并画出函数![]() 的图象;
的图象;
(2)若函数![]() 在区间
在区间![]() 上是增函数,结合函数
上是增函数,结合函数![]() 的图象,求实数
的图象,求实数![]() 的取值范围;
的取值范围;
(3)结合图象,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com