
【题目】已知a,b为常数,且a≠0,f(x)=ax2+bx,f(2)=0,方程f(x)=x有两个相等实数根.
(1)求函数f(x)的解析式;
(2)当x∈[1,2]时,求f(x)的值域;
【答案】(1) f(x)=-![]() x2+x. (2)
x2+x. (2) ![]()
【解析】
(1)由f(2)=0,方程f(x)=x有两个相等实数根,建立关于![]() 的二元一次方程组,求出
的二元一次方程组,求出![]() 的值;(2)利用二次函数的单调性求f(x)的值域.
的值;(2)利用二次函数的单调性求f(x)的值域.
解:(1)![]() f(x)=ax2+bx.
f(x)=ax2+bx.
由f(2)=0,得4a+2b=0,即2a+b=0①
方程f(x)=x,即ax2+bx=x,
即ax2+(b-1)x=0有两个相等实根,且a≠0,
∴b-1=0,∴b=1,代入①得a=-![]() .
.
∴f(x)=-![]() x2+x.
x2+x.
(2)由(1)知f(x)=-![]() (x-1)2+
(x-1)2+![]() .
.
显然函数f(x)在[1,2]上是减函数,
∴x=1时,ymax=![]() ,x=2时,ymin=0.
,x=2时,ymin=0.
∴x∈[1,2]时,函数的值域是![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 的图象恒过(0,0)和(1,1)两点,则称函数
的图象恒过(0,0)和(1,1)两点,则称函数![]() 为“0-1函数”.
为“0-1函数”.
(1)判断下面两个函数是否是“0-1函数”,并简要说明理由:
①![]() ; ②
; ②![]() .
.
(2)若函数![]() 是“0-1函数”,求
是“0-1函数”,求![]() ;
;
(3)设![]()
![]() ,定义在R上的函数
,定义在R上的函数![]() 满足:① 对
满足:① 对![]()
![]() ,
,![]()
![]() R,均有
R,均有![]() ;②
;② ![]() 是“0-1函数”,求函数
是“0-1函数”,求函数![]() 的解析式及实数a的值.
的解析式及实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市“网约车”的现行计价标准是:路程在![]() 以内(含
以内(含![]() )按起步价
)按起步价![]() 元收取,超过
元收取,超过![]() 后的路程按
后的路程按![]() 元/
元/![]() 收取,但超过
收取,但超过![]() 后的路程需加收
后的路程需加收![]() 的返空费(即单
的返空费(即单
价为![]() 元/
元/![]() ).
).
(1) 将某乘客搭乘一次“网约车”的费用![]() (单位:元)表示为行程
(单位:元)表示为行程![]() ,
,
单位:![]() )的分段函数;
)的分段函数;
(2) 某乘客的行程为![]() ,他准备先乘一辆“网约车”行驶
,他准备先乘一辆“网约车”行驶![]() 后,再换乘另一辆
后,再换乘另一辆
“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,且有a1=1,Sn+1=an+1(n∈N*).
(1)求数列{an}的通项an;
(2)若bn= ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)设ck= ![]() ,{ck}的前n项和为An , 是否存在最小正整数m,使得不等式An<m对任意正整数n恒成立?若存在,求出m的值;若不存在,说明理由.
,{ck}的前n项和为An , 是否存在最小正整数m,使得不等式An<m对任意正整数n恒成立?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+bx+c,且f(1)=-![]() ,3a>2c>2b,求证:
,3a>2c>2b,求证:
(1)a>0,且-3<![]() <-
<-![]() ;
;
(2)函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1,x2是函数f(x)的两个零点,则![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高二学生对“地方历史”校本课程的喜欢是否与在本地成长有关,在全校高二学生中随机抽取了20名,得到一组不完全的统计数据如下表:
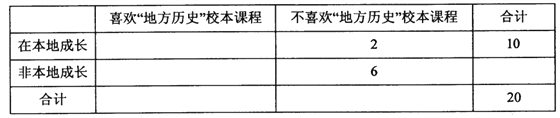
(1)补齐上表数据,并分别从被抽取的喜欢“地方历史”校本课程与不喜欢“地方历史”校本课程的学生中各选1名做进一步访谈,求至少有1名学生属于在本地成长的概率;
(2)试回答:能否在犯错误的概率不超过0.10的前提下认为“是否喜欢地方历史校本课程与在本地成长有关”.
附:

(参考公式: 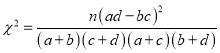 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时![]() 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米![]()
![]() (单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油![]() 升,司机的工资是每小时30元.
升,司机的工资是每小时30元.
(1)求这次行车总费用![]() 关于
关于![]() 的表达式;
的表达式;
(2)当![]() 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com