Question

球与它的外切圆柱及外切等边圆锥的体积之比为

4：6：9

．

Answer 1

分析：设出球的半径，求出球的外切圆柱的底面半径和高，外切等边圆锥的底面半径，然后求出三个体积即可得到比值．

解答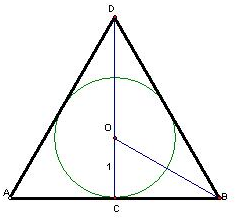：解：设球的半径为：1，
则球的外切圆柱的底面半径为：1，高为：2，
对于球的外切等边圆锥，如图，是它们的轴截面图，
在△BCD中，OC=1，∠CBO=30°，∴BC=

3

，
在△BCD中，∠CBD=60°，∴CD=3．即球的外切等边圆锥的底面半径为：

3

，圆锥的高为：3．
所以球的体积为：

4π

3

；
圆柱的体积：2×π1²=2π
圆锥 的体积：

1

3

×π（

3

）²×3=3π
一个球与它的外切圆柱、外切等边圆锥（圆锥的轴截面为正三角形）的体积之比：4：6：9
故答案为：4：6：9．

点评：本题考查球的体积，圆锥，圆柱的体积，找出三个几何体之间的关系，利用公式解题即可，考查计算能力，是基础题．