
【题目】已知函数f(x)=sinωx+λcosωx,其图象的一个对称中心到最近的一条对称轴的距离为 ![]() ,且在x=
,且在x= ![]() 处取得最大值.
处取得最大值.
(1)求λ的值.
(2)设 ![]() 在区间
在区间 ![]() 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
【答案】
(1)解:f(x)=sinωx+λcosωx= ![]() sin(ωx+φ),其中tanφ=λ;
sin(ωx+φ),其中tanφ=λ;
由题可得 ![]() =
= ![]() ,
,
∴T=π,
∴ω= ![]() =2,
=2,
∵x= ![]() 处取得最大值,
处取得最大值,
∴ ![]() +φ=
+φ= ![]() ,
,
∴φ= ![]() ,
,
∴λ=tan ![]() =
= ![]()
(2)解:由(1)可得f(x)=2sin(2x+ ![]() ),
),
∴ ![]() =2asin(2x+
=2asin(2x+ ![]() )+cos(4x﹣
)+cos(4x﹣ ![]() )
)
=2asin(2x+ ![]() )+2cos2(2x﹣
)+2cos2(2x﹣ ![]() )﹣1
)﹣1
=2asin(2x+ ![]() )+2sin2(2x+
)+2sin2(2x+ ![]() )﹣1;
)﹣1;
设t=sin(2x+ ![]() ),其中x∈(
),其中x∈( ![]() ,
, ![]() ),
),
∴2x+ ![]() ∈(
∈( ![]() ,π),
,π),
0<sin(2x+ ![]() )<
)< ![]() ,
,
函数t=sin(2x+ ![]() )是单调减函数,且0<t<
)是单调减函数,且0<t< ![]() ;
;
∴函数g(t)=2t2+2at﹣1,在对称轴t=﹣ ![]() 的左侧单调递减,
的左侧单调递减,
令﹣ ![]() ≥
≥ ![]() ,解得a≤﹣1,
,解得a≤﹣1,
∴a的取值范围是a≤﹣1
【解析】(1)化简f(x)为正弦型函数,利用函数的周期和最值求出ω、λ的值;(2)由f(x)写出g(x)的解析式,利用换元法和复合函数的单调性,即可求出a的取值范围.
【考点精析】关于本题考查的两角和与差的正弦公式,需要了解两角和与差的正弦公式:![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛中获胜的事件是独立的,并且获胜的概率均为 ![]() .
.
(1)求这支篮球队首次获胜前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好获胜3场的概率;
(3)求这支篮球队在6场比赛中获胜场数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣2x , g(x)=lg(ax2﹣2x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
A.(﹣1,0)
B.(0,1)
C.(﹣∞,1]
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD. 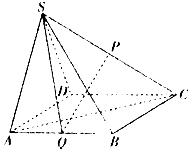
(1)求证:PQ∥平面SAD;
(2)求证:SQ⊥AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com