
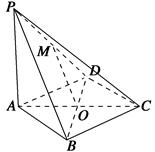
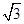 时,求PB的长.
时,求PB的长.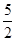
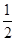 ×AB×AD×sin 60°=2×2×
×AB×AD×sin 60°=2×2×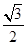 =2
=2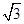 .
.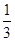 ×2
×2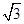 ×PA=
×PA=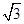 ,解得PA=
,解得PA=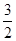 .又∵PA⊥平面ABCD,AB?平面ABCD,∴PA⊥AB.在Rt△PAB中,PB=
.又∵PA⊥平面ABCD,AB?平面ABCD,∴PA⊥AB.在Rt△PAB中,PB= 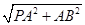 =
=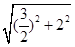 =
=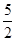 .
.

科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,点F是PB的中点,点E在边BC上移动
,点F是PB的中点,点E在边BC上移动
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= .
,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= .
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, 是两条不同的直线,
是两条不同的直线, ,
, ,
, 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题: ,
, ,
, ,则
,则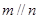 ;
; ,
, ,则
,则 ;
; ,
, ,
, ,则
,则 ;
; ,
, ,
, ,则
,则 .
.| A.①④ | B.①③ | C.②③④ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①或② | B.②或③ | C.①或③ | D.只有② |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
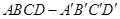 的棱长为1,
的棱长为1,  分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 交于
交于 ,设
,设 ,
, ,给出以下四个命题:
,给出以下四个命题: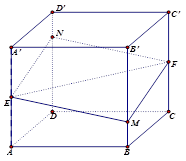

 平面
平面 ;
; 时,四边形
时,四边形 的面积最小;
的面积最小;  周长
周长 ,
, 是单调函数;
是单调函数; 的体积
的体积 为常函数;
为常函数;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com