
【题目】已知椭圆 ![]() +y2=1(a>1),过直线l:x=2上一点P作椭圆的切线,切点为A,当P点在x轴上时,切线PA的斜率为±
+y2=1(a>1),过直线l:x=2上一点P作椭圆的切线,切点为A,当P点在x轴上时,切线PA的斜率为± ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)设O为坐标原点,求△POA面积的最小值.
【答案】解:(Ⅰ)当P点在x轴上时,P(2,0),PA: ![]() ,
, ,
,
△=0a2=2,椭圆方程为 ![]() ;
;
(Ⅱ)设切线为y=kx+m,设P(2,y0),A(x1 , y1),
则 ![]() (1+2k2)x2+4kmx+2m2﹣2=0△=0m2=2k2+1,…7
(1+2k2)x2+4kmx+2m2﹣2=0△=0m2=2k2+1,…7
且 ![]() ,y0=2k+m
,y0=2k+m
则 ![]() ,
,
PA直线为 ![]() ,A到直线PO距离
,A到直线PO距离  ,
,
则 ![]()
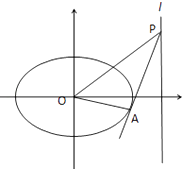
= 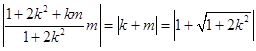 ,
,
∴(S﹣k)2=1+2k2k2+2Sk﹣S2+1=0,![]() ,此时
,此时 ![]() .
.
【解析】(Ⅰ)由P在x轴设出P点坐标及直线PA方程,将PA方程与椭圆方程联立,整理关于x的一元二次方程,△=0求得a2 , 即可求得椭圆方程;(Ⅱ)设出切线方程和点P及点A的坐标,将切线方程代入椭圆方程,求得关于x的一元二次方程,△=0,求得A和P点的坐标,求得|PA|及A到直线OP的距离,根据三角形的面积公式求得S=|k+ ![]() |,平方整理关于k的一元二次方程,△≥0,即可求得S的最小值.
|,平方整理关于k的一元二次方程,△≥0,即可求得S的最小值.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】△ABC中,已知角A,B,C所对的边分别为a,b,c, ![]() +
+ ![]() =
= ![]() ,b=4,且a>c.
,b=4,且a>c.
(1)求ac的值;
(2)若△ABC的面积为2 ![]() ,求a,c的值.
,求a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:四棱锥P﹣ABCD中,PD=PC,底面ABCD是直角梯形AB⊥BC,AB∥CD,CD=2AB,点M是CD的中点.
(1)求证:AM∥平面PBC;
(2)求证:CD⊥PA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,AB为椭圆的一条弦(不经过原点),直线y=kx(k>0)经过弦AB的中点,与椭圆C交于P,Q两点,设直线AB的斜率为k1 .
,AB为椭圆的一条弦(不经过原点),直线y=kx(k>0)经过弦AB的中点,与椭圆C交于P,Q两点,设直线AB的斜率为k1 . 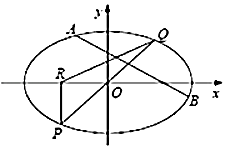
(1)若点Q的坐标为(1, ![]() ),求椭圆C的方程;
),求椭圆C的方程;
(2)求证:k1k为定值;
(3)过P点作x轴的垂线,垂足为R,若直线AB和直线QR倾斜角互补.若△PQR的面积为2 ![]() ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2017年初的时候,国家政府工作报告明确提出,2017年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,6月至11月的用煤量如下表所示:

(1)由于某些原因, ![]() 中一个数据丢失,但根据6至9月份的数据得出少样本平均值是3.5,求出丢失的数据;
中一个数据丢失,但根据6至9月份的数据得出少样本平均值是3.5,求出丢失的数据;
(2)请根据6至9月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与10月11月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过0.3,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?(参考公式:线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=92n﹣1 , n∈N* .
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn , 若不等式Sn>tan﹣1,对一切n∈N*恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 和
和![]() .
.
(![]() )若
)若![]() ,
, ![]() 是正方形一条边上的两个顶点,求这个正方形过顶点
是正方形一条边上的两个顶点,求这个正方形过顶点![]() 的两条边所在直线的方程;
的两条边所在直线的方程;
(![]() )若
)若![]() ,
, ![]() 是正方形一条对角线上的两个顶点,求这个正方形另外一条对角线所在直线的方程及其端点的坐标.
是正方形一条对角线上的两个顶点,求这个正方形另外一条对角线所在直线的方程及其端点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在无穷数列![]() 中,
中, ![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
, ![]() ,设
,设![]() ,记使得
,记使得![]() 成立的
成立的![]() 的最大值为
的最大值为![]() .
.
(![]() )设数列
)设数列![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,写出
,写出![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )若
)若![]() 为等比例数列,且
为等比例数列,且![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com