
����Ŀ��ij���ͳ�����Ե��쵱�칺����![]() Ԫ�Ĺ˿ͽ��л����������涨���˿�ת��ʮ���ȷ����ʵؾ��ȵ�Բ��ת�̣���ͼ������ת��ֹͣת��ʱ����ָ��ָ������������˿Ϳ���ȡ�������Ӧ����λ��Ԫ���ij��д���ȯ������ת��ÿ��ת���Ľ������Ӱ�죮
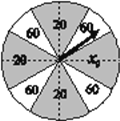
Ԫ�Ĺ˿ͽ��л����������涨���˿�ת��ʮ���ȷ����ʵؾ��ȵ�Բ��ת�̣���ͼ������ת��ֹͣת��ʱ����ָ��ָ������������˿Ϳ���ȡ�������Ӧ����λ��Ԫ���ij��д���ȯ������ת��ÿ��ת���Ľ������Ӱ�죮
������![]() ����˿�ת��һ��ת�̻��
����˿�ת��һ��ת�̻��![]() Ԫ����ȯ�ĸ��ʣ�
Ԫ����ȯ�ĸ��ʣ�
����ij�˿Ϳ�������ת������ת�̲������Ӧ��������![]() ʱ����ù˿͵�һ�λ�ô���ȯ�������ڵڶ��λ�ô���ȯ�����ĸ��ʣ�
ʱ����ù˿͵�һ�λ�ô���ȯ�������ڵڶ��λ�ô���ȯ�����ĸ��ʣ�
�������ǹ˿�ÿ��ת��ת�̻�ô���ȯ�����Ϊ![]() ����
����![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() �ķ�����С��
�ķ�����С��
�����۲�Ҫ��֤����
���𰸡�(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
������������������������ü��θ��͵ĸ��ʹ�ʽ������⣻�������û����¼��ĸ��ʹ�ʽ��������¼�ͬʱ�����ĸ��ʹ�ʽ������⣻�������÷��ʽ�������.
����������������¼�![]() Ϊ���˿�ת��һ��ת�̻��
Ϊ���˿�ת��һ��ת�̻��![]() Ԫ����ȯ����
Ԫ����ȯ����
������֪![]() .
.
�������¼�![]() Ϊ���˿͵�һ�λ�ô���ȯ�����ڵڶ��λ�õĴ���ȯ�������
Ϊ���˿͵�һ�λ�ô���ȯ�����ڵڶ��λ�õĴ���ȯ�������
���¼�![]() Ϊ���ù˿͵�
Ϊ���ù˿͵�![]() ת��ת�̻�õij��д���ȯ���Ϊ
ת��ת�̻�õij��д���ȯ���Ϊ![]() ����
���� ![]() .
.
������֪�� ![]() ��
�� ![]() .
.
���![]()
![]()
![]() .
.
������![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��
��
��1���ж�f��x���ڣ�0��+�ޣ��ĵ����ԣ�
��2����x��0��֤������ex��1��ln��x+1����x2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|f��x��=lg��x��1��+ ![]() }������B={y|y=2x+a��x��0}��
}������B={y|y=2x+a��x��0}��
��1����a= ![]() ����A��B��
����A��B��
��2����A��B=����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڣ� ![]() ��
�� ![]() ��n��չ��ʽ�У���6��Ϊ�����
��n��չ��ʽ�У���6��Ϊ�����
��1����n��
��2����x2���ϵ����
��3����չ��ʽ�����е������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �Ķ���˵㵽�ҽ���
�Ķ���˵㵽�ҽ���![]() �ľ���Ϊ2��
�ľ���Ϊ2��
����������Բ![]() �ķ��̣�
�ķ��̣�
����������![]() ��ֱ�߽���Բ
��ֱ�߽���Բ![]() ��
��![]() ���㣬��ֱ��
���㣬��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
�� ![]() ����֤��
����֤�� ![]() Ϊ��ֵ��
Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=Asin����x+�գ���x��R������A��0���أ�0��0���գ� ![]() ����ͼ����x���������������ľ���Ϊ
����ͼ����x���������������ľ���Ϊ ![]() ����ͼ����һ����͵�ΪM��
����ͼ����һ����͵�ΪM�� ![]() ����2���� ������f��x���Ľ���ʽ��
����2���� ������f��x���Ľ���ʽ��
������f��x���ĵ����������䣻
����x��[ ![]() ��
�� ![]() ]ʱ����f��x����ֵ��
]ʱ����f��x����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֪����y= ![]() �Ķ�����Ϊ�� ��
�Ķ�����Ϊ�� ��
A.�����ޣ�1]
B.�����ޣ�2]??
C.�����ޣ��� ![]() ���ɣ���
���ɣ��� ![]() ��1]
��1]
D.�����ޣ��� ![]() ���ȣ���
���ȣ��� ![]() ��1]
��1]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������n��Կ�ף�����ֻ��һ�ѿ��Դ��ţ�������Ľ����Կ������Կ�����Կ����һ�ߣ��Կ�����XΪ�����������P��X=k��=�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}��ǰn���ΪSn �� ��a2=3��S5=25��
��1��������{an}��ͨ�ʽan��
��2��������{ ![]() }��ǰn���ΪTn �� �Ƿ����k��N* �� ʹ�õ�ʽ2��2Tk=
}��ǰn���ΪTn �� �Ƿ����k��N* �� ʹ�õ�ʽ2��2Tk= ![]() �����������ڣ����k��ֵ���������ڣ�˵�����ɣ�
�����������ڣ����k��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com