
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 和曲线
和曲线![]() 交于A,B两点(点A在第二象限).过A作斜率为
交于A,B两点(点A在第二象限).过A作斜率为![]() 的直线
的直线![]() 交曲线M于点C(不同于点A),过点
交曲线M于点C(不同于点A),过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于E,F两点,且
于E,F两点,且![]() .
.
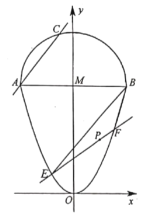
(I)求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() 的面积为S,求
的面积为S,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国营企业集团公司现有员工1000名,平均每人每年创造利润10万元.为了激化内部活力,增强企业竞争力,集团公司董事会决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业;调整后,他们平均每人每年创造利润
)名员工从事第三产业;调整后,他们平均每人每年创造利润![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() %.
%.
(Ⅰ)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(Ⅱ)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则实数![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆![]() :
:![]() (
(![]() )过点
)过点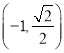 ,离心率为
,离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,
,![]() ,且过焦点
,且过焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 的坐标为
的坐标为![]() ,设直线
,设直线![]() 与直线
与直线![]() 的斜率分别为
的斜率分别为![]() ,试证明:
,试证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,某校在高中生中随机抽取100名学生进行了问卷调查,得到如下列联表:
喜欢数学 | 不喜欢数学 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 50 | 100 |
(1)请将上面的列联表补充完整;
(2)能否在犯错误的概率不超过0.001的前提下认为“喜欢数学”与性别有关?说明你的理由;
(3)若在接受调查的所有男生中按照“是否喜欢数学”进行分层抽样,现随机抽取6人,再从6人中抽取3人,求至少有1人“不喜欢数学”的概率.
下面的临界值表供参考:
| 0.05 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式: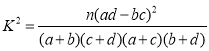 ,其中
,其中![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com