
【题目】已知函数f(x)=x3-3x2-9x+2.
(1) 求函数![]() 的单调区间;
的单调区间;
(2) 求函数![]() 在区间[-2,2]上的最小值.
在区间[-2,2]上的最小值.
【答案】(1)f(x)的单调递增区间是(-∞,-1),(3,+∞);单调递减区间是(-1,3);(2)-20.
【解析】
(1)求导后,令f′(x)=0,得x=-1或x=3,再列表,由表格可得结果;
(2)根据函数![]() 在区间[-2,2]上的单调性可求得最小值.
在区间[-2,2]上的单调性可求得最小值.
f′(x)=3x2-6x-9=3(x+1)(x-3),
令f′(x)=0,得x=-1或x=3,
当x变化时,f′(x),f(x)在区间R上的变化状态如下:
|
|
|
| 3 |
|
| + | 0 | - | 0 | + |
|
| 极大 |
| 极小 |
|
所以f(x)的单调递增区间是(-∞,-1),(3,+∞);单调递减区间是(-1,3);
(2)解:因为f(-2)=0,f(2)=-20,
再结合f(x)的单调性可知,
函数f(x)在区间[-2,2]上的最小值为-20.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知非单调数列{an}是公比为q的等比数列,a1=![]() ,其前n项和为Sn(n∈N*),且满足S3+a3,S5+a5,S4+a4成等差数列.
,其前n项和为Sn(n∈N*),且满足S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式和前n项和Sn;
(2)bn=![]() +
+![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形公园![]() 中,
中,![]() ,
,![]() ,
,![]() ,公园的左下角阴影部分为以
,公园的左下角阴影部分为以![]() 为圆心,半径为
为圆心,半径为![]() 的
的![]() 圆面的人工湖,现设计修建一条与圆相切的观光道路
圆面的人工湖,现设计修建一条与圆相切的观光道路![]() (点
(点![]() 分别在
分别在![]() 与
与![]() 上),
上),![]() 为切点,设
为切点,设![]() .
.

(1)试求观光道路![]() 长度的最大值;
长度的最大值;
(2)公园计划在道路![]() 的右侧种植草坪,试求草坪
的右侧种植草坪,试求草坪![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值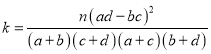
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+![]() )+cos(2x﹣
)+cos(2x﹣![]() )+cos2x﹣sin2x,x∈R.
)+cos2x﹣sin2x,x∈R.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)求函数f(x)在区间[﹣![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面四边形MNPQ中,MN=![]() ,MP=1,MP⊥MN,PQ⊥QM.
,MP=1,MP⊥MN,PQ⊥QM.
(Ⅰ)若PQ=![]() ,求NQ的值;
,求NQ的值;
(Ⅱ)若∠MQN=30°,求sin∠QMP的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的焦点,椭圆的右准线
的焦点,椭圆的右准线![]() 与
与![]() 轴交于
轴交于![]() 点,若
点,若![]() ,且
,且![]() .
.

(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 、
、![]() 作互相垂直的两直线分别与椭圆交于
作互相垂直的两直线分别与椭圆交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求四边形
四点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com