
【题目】某学校积极开展“服务社会,提升自我”的志愿者服务活动,九年级的五名同学(三男两女)成立了“交通秩序维护”小分队.若从该小分队中任选两名同学进行交通秩序维护,则恰是一男一女的概率是________.
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在R上的两个周期函数,
是定义在R上的两个周期函数,![]() 的周期为4,
的周期为4,![]() 的周期为2,且
的周期为2,且![]() 是奇函数.当
是奇函数.当![]() 时,
时,![]() ,
, ,其中k>0.若在区间(0,9]上,关于x的方程
,其中k>0.若在区间(0,9]上,关于x的方程![]() 有8个不同的实数根,则k的取值范围是_____.
有8个不同的实数根,则k的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,某窑洞窗口形状上部是圆弧![]() ,下部是一个矩形
,下部是一个矩形![]() ,圆弧
,圆弧![]() 所在圆的圆心为O,经测量
所在圆的圆心为O,经测量![]() 米,
米,![]() 米,
米,![]() ,现根据需要把此窑洞窗口形状改造为矩形
,现根据需要把此窑洞窗口形状改造为矩形![]() ,其中E,F在边
,其中E,F在边![]() 上,G,H在圆弧
上,G,H在圆弧![]() 上.设
上.设![]() ,矩形
,矩形![]() 的面积为S.
的面积为S.
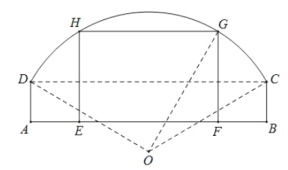
(1)求矩形![]() 的面积S关于变量
的面积S关于变量![]() 的函数关系式;
的函数关系式;
(2)求![]() 为何值时,矩形
为何值时,矩形![]() 的面积S最大?
的面积S最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() 、
、![]() ,都有
,都有![]() ,
,![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“
为“![]() 函数”.
函数”.
(1)试判断函数![]() 与
与![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)若函数![]() 为“
为“![]() 函数”,求实数
函数”,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 为“
为“![]() 函数”,且
函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:![]() 的焦点为F,经过点F的直线与抛物线交于A、B两点.
的焦点为F,经过点F的直线与抛物线交于A、B两点.
(1)若![]() ,求线段
,求线段![]() 中点M的轨迹方程;
中点M的轨迹方程;
(2)若直线AB的方向向量为![]() ,当焦点为
,当焦点为![]() 时,求
时,求![]() 的面积;
的面积;
(3)若M是抛物线C准线上的点,求证:直线![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 点.
点.![]() 为椭圆上的一动点,
为椭圆上的一动点,![]() 面积的最大值为
面积的最大值为![]() .过点
.过点![]() 的直线
的直线![]() 被椭圆截得的线段为
被椭圆截得的线段为![]() ,当
,当![]() 轴时,
轴时,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 上任取两点A,B,以
上任取两点A,B,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .若
.若![]() ,则
,则![]() 是否为定值?若是,求出定值;如不是,请说明理由.
是否为定值?若是,求出定值;如不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com